不确定有限自动机是确定有限自动机DFA的一般化,其定义与DFA类似。不确定有限自动机的基本特征在于,当一个状态遇到同一个输入符号时,可能有多种不同的转换。
一个不确定有限自动机(Nondeterministic Finite Automata,NFA)也是一个五元组,形如:
M=(S,Σ,δ,S0,F)

NFA组成
其中:
(1)S是一个有限状态集;
(2)Σ是一个有穷输入字母表;
(3)δ是状态转换函数,是在S×Σ*到S的子集的一个映射,即:
δ:S×Σ*→2S
(4)S0是一个非空初态集,且S0⊆S;
(5)F是—个终态集,可以为空,且F⊆S。
NFA可以用状态转换图来表示,结点表示状态,有标记的弧代表转换函数。一个含有m个状态,n个输入字符的NFA表示的状态转换图:有m个状态结点,每个结点可射出若干条弧与其他结点相连接,每条弧用Σ上一个字(这些字可以相同,也可以是ε)来标记(称为输入字)。整个图至少有一个初态结点以及若干个(可以为0)终态结点,某些结点即可以是初态结点,又可以是终态结点。
例3.4 对于正规式0(0|1)*0的NFA,如图3-7所示。图中,在状态1处有两个标注为0的转换,一个到达状态1,另一个到达状态2。

图3-7 0(0|1)*0的NFA
对于Σ*中的任何字符串α,若存在一条从初态结点到某一终态结点的通路,且这条通路上所有弧的标记字依序连接成的字符串(忽略标记为ε的弧)等于α,则称α可为NFA M所识别(读出或接受)。若M的某些结点既是初态结点又是终态结点,或者存在一条从某个初态结点到某个终态结点的通路,其上所有弧的标记均为ε,则空字ε可为M所接受。NFA M所能识别的字符串的全体记为L(M)。
容易看出,DFA是NFA的特例,那么,如何从NFA得到等价的DFA呢?这需要用到NFA的确定化技术。
对于任意两个有限自动机M和M,若有L(M)=L(M),则称M和M是等价的。对于每个NFA M,都存在着一个DFA M,使得L(M)=L(M)。与某一NFA等价的DFA不唯一。

状态集合的运算
从NFA构造等价的DFA,通常使用子集法,其基本思路是:DFA的每一个状态与NFA的一组状态相对应,用DFA的一个状态去记录在NFA读入一个输入符号后可能达到的状态集合。下面先介绍一下与状态集合I有关的几个运算。
(1)状态集合I的ε-闭包,记为ε_Closure(I),定义为:
·若q∈I,则q∈ε_Closure(I);
·若q∈I,则从q出发经任意条ε边而能到达的状态q都属于ε_Closure(I)。
(2)状态集合I的α弧转换,记为Iα,定义为:
Iα=ε_Closure(J)
其中,J是所有那些可从I中的某一状态结点出发经过一条α弧而到达的状态的全体。
例如,从图3-8中可以得到以下结果:

图3-8 一个NFA的例子
若I1={1},则ε_Closure(I1)={1,2};
若I2={5},则ε_Closure(I2)={5,6,2};(https://www.xing528.com)
若I3={1,2},则J={5,3,4},于是有I3a=ε_Closure({5,3,4})={2,3,4,5,6,7,8}。
将NFA确定化,需要经过两个步骤。
首先,改造NFA的状态图。由于NFA的初态和终态结点都可能有多个,而且每条弧上的标记可能是Σ*上的一个字符串,因此,需要将其改造为只有一个初态结点和一个终态结点,且每条弧上的标记只能是单个输入符号或者ε的状态图。具体做法是:
(1)增加状态X和Y,使其成为新的唯一的初态和终态。从X引ε弧到原初态结点,从原终态结点引ε弧到Y结点。
(2)依据图3-9中的规则对状态图进行替换,不断重复这一过程,直到图中每条边上的标记转化为Σ上的单个符号或者ε为止。

图3-9 替换规则

NFA到DFA的转化
其次,使用子集法将改造后的NFA确定化。具体做法是:
(1)对Σ={a1,…,ak},构造一个k+1列的状态转换表,列为状态,行为输入字符。置该表的首行首列为ε_Closure(X),X为第一步完成后的唯一的开始状态。
(2)若某行的第一列的状态已确定为I,则计算第i+1(i=1,2,…,k)列的值为Iai,然后,检查该行上的所有状态子集,看其是否已在第一列出现。若未出现,则将其添加到后面的空行上。重复这一过程,直到所有状态子集均在第一列中出现为止。
(3)将每个状态子集视为一个新的状态,即可得到一个DFA。初态就是首行首列的状态,终态就是含有原有终态的所有状态。
例3.5 将图3-10中NFA确定化。
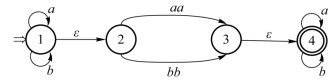
图3-10 接受包含aa或bb的字的NFA
首先,改造NFA的状态图,改造后的结果如图3-11所示。
其次,使用子集法将改造后的NFA确定化。先构造一个3列的状态转换表,ε_Closure(X)作为该表的首行首列值,由图3-11可知,ε_Closure(X)为{X,1,2};接着,求该集合的Ia和Ib,如表3-3所示。

图3-11 改造后的NFA
表3-3 状态转换表(1)

检查该行上所有表项的值,看其是否已在第一列出现过,若没有出现,则将其添加到第一列。比如,表3-3中的{1,2,3}和{1,2,4}在第一列都没有出现过,将其加入第一列,继续求其Ia和Ib的值,重复这一过程,最后得到表3-4。
表3-4 状态转换表(2)

重命名所有状态,如表3-5所示。
表3-5 状态转换表(3)

据表3-5,可以得到与给定的NFA等价的DFA,如图3-12所示。

图3-12 与图3-11等价的DFA
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




