确定有限自动机（DFA）-编译原理与实践

有限自动机，也称作有穷自动机，是一种识别正规集的装置，它能够准确识别正规文法所定义的语言和正规式所表示的集合。有限自动机分为确定有限自动机和不确定有限自动机两种，下面首先介绍确定有限自动机。

一个确定有限自动机（Deterministic Finite Automata，DFA）是一个五元组，形如：

M=(S,Σ,δ,S0,F)

DFA组成

其中：

（1）S是一个有限集，它的每个元素称为一个状态；

（2）Σ是一个有穷字母表，它的每个元素称为一个输入字符；

（3）δ是状态转换函数，是在S×Σ→S上的单值部分映射。δ（s1，a）=s2表示当现行状态为s1，输入字符为a时，将转换到下一状态s2。我们称s2为s1的一个后继状态；

（4）S0是唯一的初态，且S0∈S；

（5）F是—个终态集，可以为空，且F⊆S。

显然，一个DFA可用—个矩阵表示，该矩阵的列表示状态，行表示输入字符，矩阵元素表示δ（s，a）的值。这样的矩阵称为状态转换矩阵。例如，有DFA M=（{0，1，2，3}，{a，b}，δ，0，{3}），其中，δ为：

δ(0,a)=1 δ(0,b)=2(www.xing528.com)

δ(1,a)=3 δ(1,b)=2

δ(2,a)=1 δ(2,b)=3

δ(3,a)=3 δ(3,b)=3

DFA M的状态转换矩阵如表3-2所示。

表3-2　M的状态转换矩阵

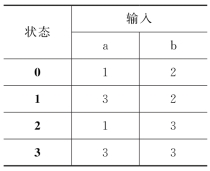
一个DFA既可以表示成状态转换矩阵的形式，也可以表示成一张（确定的）状态转换图。假定DFA M含有m个状态和n个输入字符，那么，其状态转换图则含有m个状态结点，每个结点至多有n条箭弧射出与其他结点相连接，每条箭弧用Σ中的一个不同输入字符做标记，整张图含有唯一的一个初态结点和若干个（可以为0）终态结点。初态结点冠以双箭头“⇒”，终态结点用双圈表示，若δ（si，a）=sj，则从结点si到结点sj画标记为a的弧。图3-6即为上例中DFA M对应的状态转换图。

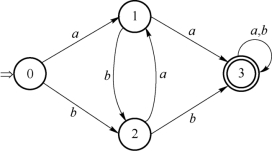
图3-6　M的状态转换图

DFA的表示方式

对于Σ*中的任何字符串α，若存在一条从初态结点到某一终态结点的通路，且这条通路上所有弧的标记符连接成的字符串等于α，则称α可为DFA M所识别（读出或接受）。若M的初态结点同时又是终态结点，则空字ε可为M所识别。DFA M所能识别的字符串的全体记为L（M）。