编译原理与实践：上下文无关文法

文法是一种描述语言的语法结构的形式规则（即语法规则），这些规则必须准确而且易于理解，同时，应当有相当强的描述能力，足以描述各种不同的语法结构。所谓上下文无关文法是指这样一种文法，它所定义的语法范畴（或语法单位）是完全独立于这种范畴可能出现的环境的。我们知道，自然语言中的一个句子、一个词甚至一个字，其语法性质和所处的上下文往往有密切的关系，因此，上下文无关文法不宜于描述任何自然语言，但是对于如今的高级程序设计语言来说，这种文法基本上是够用了。在程序语言中，我们完全可以对各个语法单位独立进行处理，而不必考虑它所处的上下文。例如，当碰到一个算术表达式时，我们只需分析该表达式的语法是否正确即可，而不用“左顾右盼”地考虑其所处的上下文环境。以后，凡“文法”一词若无特殊说明，则均指上下文无关文法。

下面，我们从一个具体的英文语句的分析入手，逐步引出文法的形式化定义方法。例如，有这样一个句子：

文法包含

The grey wolf will eat the goat.

现给出如下的语法规则：

＜句子＞→＜主语＞＜谓语＞ ＜主语＞→＜冠词＞＜形容词＞＜名词＞

＜冠词＞→the ＜形容词＞→grey

＜谓语＞→＜动词＞＜直接宾语＞ ＜动词＞→＜助动词＞＜动词原形＞

＜助动词＞→will ＜动词原形＞→eat

＜直接宾语＞→＜冠词＞＜名词＞ ＜名词＞→wolf

＜名词＞→goat

其中，“→”表示“由……组成”或“定义为”。很明显，上述句子是一个语法上正确的句子。换句话说，根据这些规则，我们可以得到上述句子，具体分析过程如下：

＜句子＞⇒＜主语＞＜谓语＞

⇒＜冠词＞＜形容词＞＜名词＞＜谓语＞

⇒the＜形容词＞＜名词＞＜谓语＞

⇒the grey＜名词＞＜谓语＞

⇒the grey wolf＜谓语＞

⇒the grey wolf＜动词＞＜直接宾语＞

⇒the grey wolf＜助动词＞＜动词原形＞＜直接宾语＞

⇒the grey wolf will＜动词原形＞＜直接宾语＞

⇒the grey wolf will eat＜直接宾语＞

⇒the grey wolf will eat＜冠词＞＜名词＞

⇒the grey wolf will eat the＜名词＞

⇒the grey wolf will eat the goat

由以上分析可以看出，判断一个句子语法上是否正确的过程，实际上就是从＜句子＞出发，反复使用上述语法规则“→”右边的部分替换左边部分的过程。如果最终通过替换产生了这个句子，则说明它是一个语法上正确的句子。

然而，有时语法上正确的句子语义未必正确，比如，根据上述语法规则我们也可以得到如下的句子：

＜句子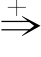＞the grey wolf will eat the wolf

＜句子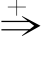＞the grey goat will eat the wolf

＜句子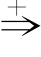＞the grey goat will eat the goat

很明显，这三个句子都不符合语义要求。至于如何分析语义，我们将在第6章中进行介绍。

文法组成

上述自然语言的定义就是一个上下文无关文法。归纳起来，一个上下文无关文法G包括四个组成部分：一组终结符号，一组非终结符号，一个开始符号以及一组产生式。

终结符号：指组成语言的基本符号，如上例中的“the”“wolf”和“eat”等。在程序语言中就是指各种单词符号，如保留字、标识符、常数、算符和界符等。从语法分析的角度来看，终结符号是—个语言不可再分的基本符号。终结符的集合是非空有限集，往往用VT来表示。

非终结符号：指用来表示语法范畴的符号，如上例中的＜句子＞、＜主语＞和＜谓语＞等。—个非终结符表示一个语法概念，是一个类（或集合）的记号，而非一个个体记号。在程序语言中的非终结符号有“算术表达式”“赋值语句”以及“分程序”等。非终结符号的集合也是非空有限集，通常用VN表示，于是有文法G的字母表V=VT∪VN，且VT∩VN=φ。

开始符号：是一个特殊的非终结符，用S来表示，代表所定义的语言中我们最终感兴趣的语法范畴，如上例中的＜句子＞。在程序语言中，开始符号就是“程序”，“程序”是我们最终感兴趣的语法范畴，而其他语法范畴都是用来为“程序”服务的。

产生式：是按一定格式书写的、用来定义语法范畴的规则。产生式也称为规则，一般具有如下的形式：

A→α或A∷=α

其中，“→”或“∷=”的左边的A是一个非终结符，即A∈VN，称为产生式的左部；右边的α是由终结符号或非终结符号组成的一个符号串，即α∈（VT∪VN）*，称为产生式的右部。如上例中的“＜句子＞→＜主语＞＜谓语＞”就是一个产生式。产生式的集合是有限集，通常用P表示。

因此，从形式上讲，一个上下文无关文法G是一个四元式（VT，VN，S，P），其中，VT是终结符集，VN是非终结符集，S是开始符号，P是产生式集合。

关于文法，需要注意以下几点：

（1）开始符号S至少必须在某个产生式的左部出现一次，且第一条产生式的左部必须是开始符号。

（2）一般用大写字母A、B、C等代表非终结符号，用小写字母a、b、c等代表终结符号，而用希腊字母α、β、γ等代表由终结符和非终结符组成的符号串。

（3）有时为了书写方便，若干个左部相同的产生式，如：(www.xing528.com)

A→α1

A→α2

︙

A→αn

可以合并为一个，即：

A→α1|α2|…|αn

其中，元符号“|”读作“或”，每个αi也称为A的一个候选式。

（4）为方便起见，书写文法时可以不用列出整个四元式的形式，只需列出产生式并指出开始符号即可。文法G也可以写成G[S]，以表示S是文法G的开始符号。

前面已经讲过，我们在判断符号串“The grey wolf will eat the goat”的语法是否正确时所采用的方法是：从文法的开始符号“＜句子＞”出发，反复使用产生式规则，将符号串中的非终结符用某个产生式的右部进行替换，直到全部展开为终结符为止，继而判断该终结符序列与输入的符号串是否相同。其实，上述替换过程就是所谓的推导过程。“推导”这一概念在文法中的地位非常重要，关于其内涵读者务必深入地予以领会。

例如，考虑下面的算术表达式文法：

文法中，仅有一个非终结符E，同时也是文法的开始符号，它代表一类算术表达式。从E出发，反复使用上述产生式规则可以推出各种各样的算术表达式来。例如，根据规则

E→E+E

可以得到

E⇒E+E

于是，我们可以说：从“E”可直接（—步地）推出“E+E”。与前面相同，“⇒”被用来表示“直接推出”，即仅推导一步。

再有，表达式（i+i）的推导过程是：

上述替换序列每前进一步总是引用一条规则，该序列被称作是从E到（i+i）的一个推导，它证明了（i+i）是文法（2.1）所定义的一个算术表达式。

严格来讲，如果A→γ是一个产生式，α、β∈（VT∪VN）*，则称αAβ⇒αγβ为一步推出或直接推出。如果α1⇒α2⇒…⇒αn，则称它是从α1到αn的一个推导。如果存在从α1到αn的一个推导，则称α1可推导出αn。

另外，如果从α1出发，经一步或若干步可推导出αn，则可以用α1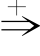αn来表示；如果从α1出发，经0步或若干步可推导出αn，则可以用α1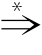αn来表示，也就是说，要么α1=α2，要么α1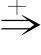αn。

给定文法G，S是G的开始符号。如果S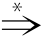α，则称α是一个句型。例如，在推导（2.2）中，E、（E）、（E+E）、（i+E）和（i+i）都是文法（2.1）的句型。若α是文法G的一个句型，且α中仅含终结符号，即α∈VT*，则称α是文法G的一个句子。在推导（2.2）中，（i+i）就是文法（2.1）的句子。

从文法G的开始符号S出发，所能推导出的句子的全体称为文法G产生的语言，记为L（G），表示如下：

L(G)={α|S⇒+α&α∈VT*}

假设有两个文法G1和G2，若L（G1）=L（G2），则称G1和G2是等价的。等价变换是文法转换的基本要求，这在文法改造或化简等操作中十分重要。

下面介绍两个简单的文法例子，一个是根据文法写出语言，另一个是根据语言找出文法。

例2.1 考虑文法G1：

S→AB

A→a A|a

B→bB|b

请指出该文法定义的语言形式。

从开始符号S出发，可以推出如下句子：

归纳得出，从S出发可推导出以至少一个a和至少一个b构成的符号串，且a的个数和b的个数之间没有任何约束，因此：

L(G1)={ambn|m,n≥1}

例2.2 试构造一个文法G2，使得

L(G2)={anbn|n≥1}

由给定的语言形式可以看出，G2要求每一个句子中的a和b的个数必须相同，即每一次a的出现必然有一个b的出现。于是，我们可以写出如下的文法G2：

S→aSb|ab

推导的过程通常并不是唯一的。推导过程中，往往会面对多个待替换的非终结符，而且，每个非终结符有可能存在着多个候选式以供选择，这些因素都给推导过程带来了不确定性。例如，在推导（2.2）中，在得到句型（E+E）后，也可以按照如下的过程进行推导：

由此可以看出，推导（2.2）和（2.3）的结果是相同的，都得到了符号串（i+i），但是，替换每个非终结符的次序却是不同的。

我们希望推导的过程是确定的，这样有助于语法结构的分析，因此，往往只考虑最左推导或最右推导。所谓最左推导，是指在整个推导过程中，每一步的替换操作都是针对句型中最左边的非终结符进行的。如果在推导的每一步都替换的是句型最右边的非终结符，则将此过程称为最右推导，或者称为规范推导。例如，文法（2.2）是最左推导，而文法（2.3）则是最右推导。

再有，以文法（2.1）为例，可以写出句子（i*i+i）的最左推导和最右推导：

最左推导：

最右推导：