代码优化器-《编译原理与实践》

代码优化器的功能是对中间代码进行优化处理。

优化的任务在于对产生的中间代码进行等价变换，以期最终能够生成时间和空间方面更为高效的目标代码。其目的主要是提高运行效率，节省存储空间。可以将优化分为两类：一类是与机器无关的优化，主要是针对中间代码进行的，包括局部优化、循环优化和全局优化等；一类是与机器有关的优化，主要是在生成目标代码时进行的，涉及如何分配寄存器以及如何选择指令等。

对于表1-3的中间代码，优化前和优化后的差异如图1-4所示。

图1-4　语句id1：=id2+id3*int1的中间代码的优化

从图中可以看出，4个四元式构成的中间代码序列经过优化后变换成了2个四元式构成的中间代码序列，其中，前两个四元式合二为一，后两个四元式也合二为一。之所以能够这样做，是因为：代码优化器发现第1个四元式只是简单地做了常数int1的类型转换工作，完全没有必要单列1个四元式，可以将转换结果直接放到第2个四元式中；同样，第4个四元式也只是简单地做了变量的赋值工作，也没有必要单独写成1个四元式，可以将第3个四元式的结果直接赋值给id1。尽管优化后仅剩下了2个四元式，但与优化前的4个四元式功能完全一致，从而说明优化过程是合理的。

下面我们再看一个较为复杂的例子。对于如下的Pascal程序片段：(www.xing528.com)

优化前和优化后的中间代码变换情况如表1-4所示。

表1-4　中间代码的优化

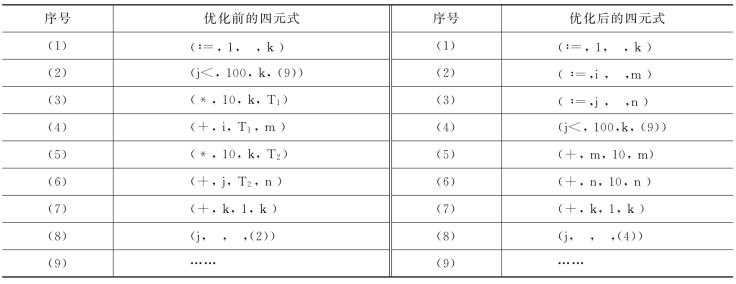
明显可以看出，优化后最终得到的目标代码的执行效率肯定会提高很多，原因是：优化前的中间代码的循环中需做300次加法和200次乘法，然而优化后的中间代码的循环中只需做300次加法；并且，对于大多数硬件来说，加法运算的执行时间要比乘法运算的执行时间短得多。

代码优化的主要依据是程序的等价变换原则。常用的优化方法主要包括合并已知量、删除公共子表达式、删除无用代码、代码外提等，这些内容将在第8章中予以介绍。