地铁隧道电磁场仿真实例

接触轨是城市轨道交通线路敷设的与轨道平行的附加轨，又称为第三轨，电能通过它输送给电动车组。运行过程中，电动车组伸出的集电靴与之接触并接收电能。

接触轨上电压额定值为DC 750 V，电压允许波动范围为500～900 V，最大持续电流有效值3 000 A，供给电动车的电流经过走行轨返回牵引变电所。其中，接触轨接牵引变电所正极线路，走行轨接牵引变电所负极线路。

由图2-24 可见，因接触轨的存在破坏了隧道内电磁场分布的对称性，为求解隧道内的电磁场分布，首先将求解域划分成不同的子空间（离散化），并计算各子空间的电磁场，再用各子空间的计算结果逼近整个隧道截面的电磁场（有限元分析方法）。

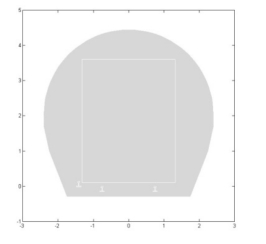
图2-24　第三轨供电方式下隧道结构图

现在以第三轨道DC 750 V 供电方式下的地铁隧道电磁场仿真为例，使用PDE 工具求解，求解步骤如下所示。

1.应用模式选择

在MATLAB 命令窗口中输入命令：pdetool，然后单击回车键，显示PDE 图形用户界面，如图2-25所示。

图2-25　PDE 图形用户界面

在“Options”菜单条中用鼠标指向“Application”选项，会弹出一个子菜单，在其中选择应用模式。电场和磁场应用模式选择如图2-26 和图2-27所示。

图2-26　电场应用模式的选择

图2-27　磁场应用模式的选择

2.建立几何模型

以北京地铁某区间以矿山法暗挖法施工的马蹄形隧道为例，隧道高度为4 460 mm，车体宽为2 650 mm，高为3 510 mm。接触轨和走行轨的相对位置如图2-28所示。

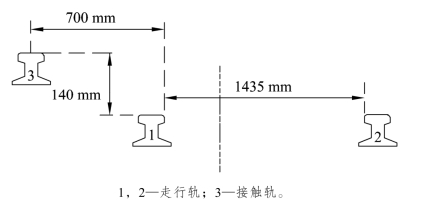
图2-28　接触轨和走形轨相对位置

在Draw 模式可以用图形交互模式或命令方式建模。在“Options”菜单中选择“Axes Limits”设置横纵坐标，在“Options”菜单中选择“Grid”选项可以在图中显示网格，单击“Grid Spacing”选项，打开对话框可以调整网格间隔大小。选择“Snap”选项，则鼠标在图中点击时，将自动选择离该点最近的网格交点。在画图之前设置上面的选项可以使绘图更方便。利用分别绘制矩形、方形、椭圆、圆形、多边形，双击所画的图形可以修改图形的坐标和尺寸。隧道无、有车时的几何模型如图2-29所示。

分析隧道电场时，接触轨和走行轨具有良好的导电性，通常可视其内部静电平衡，另外车体外壳为金属材料，因此分析静电场时的求解域是隧道内、钢轨及列车外的空间。所以在“Set Formula”文本框中输入公式，如图2-30 和图2-31所示。

分析隧道磁场时，因钢轨是良好的磁导体而列车多为铝制，其磁导率与空气十分接近，对磁场基本无影响，所以磁场分布在整个隧道空间内，整个隧道截面都列入求解域。所以在“Set Formula”文本框中的公式如图2-32 和图2-33所示。

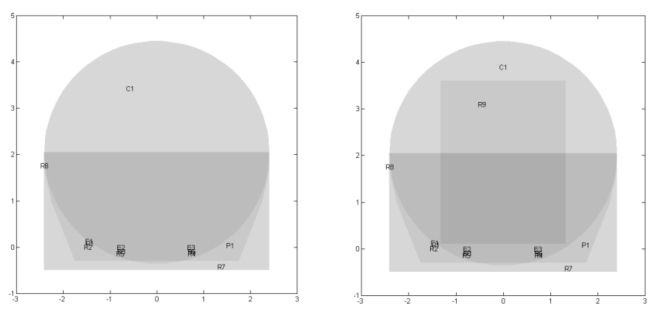
图2-29　隧道无车、有车时的几何模型

图2-30　隧道无车电场求解阈设定

图2-31　隧道有车电场求解阈设定

图2-32　隧道无车磁场求解阈设定

图2-33　道有车磁场求解阈设定

3.定义边界条件

在“Boundary”菜单中选择“Boundary mode”选项，则显示几何模型的边界。选定要裁减的线条后，使用“Boundary”菜单的“Remove Subdomain Border”命令对其进行裁减。隧道电磁场定义边界条件的界面如图2-34 和图2-35所示。

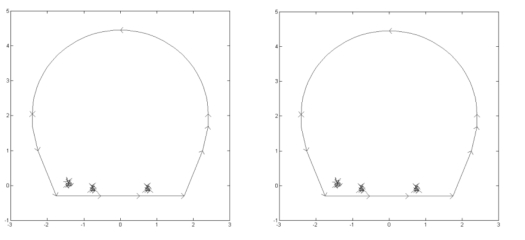
图2-34　隧道电场定义边界条件

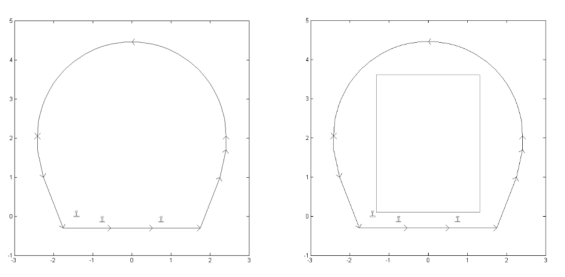
图2-35　隧道磁场定义边界条件

电场边界条件：外边界为隧道内壁，内边界为列车、接触轨、走行轨表面，内外边界都设置为Drichlet 边界条件，接触轨电位设为800 V，走行轨电位设为30 V，其余边界电位为0 V。求解电场时接触轨和走行轨边界条件的设定如图2-36 和图2-37所示。

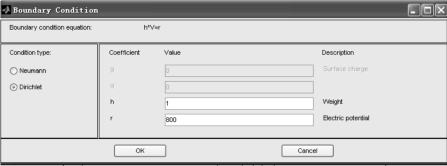
图2-36　求解电场时接触轨边界条件设定

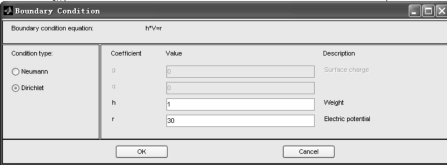
图2-37　求解电场时走行轨边界条件设定

磁场边界条件：忽略隧道外漏磁场影响，整个模型外边界设置为Drichlet 边界条件，r=0。求解磁场时的边界条件设定如图2-38所示。

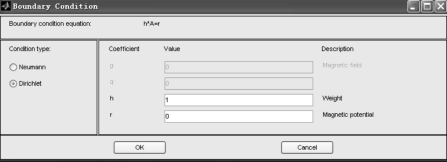
图2-38　求解磁场时的边界条件的设定

4.定义PDE 参数

在“PDE”菜单中选择“PDE mode”选项，图形将显示为PDE 模式。隧道电磁场PDE 模式图如图2-39 和图2-40所示。

图2-39　隧道电场PDE 模式图

图2-40　隧道磁场PDE 模式图

使用“show subdomain levels”命令，可以看到各带编号的子区域。双击各个子区域，可弹出求解区域设置的对话框。静电场和静磁场方程均为椭圆形方程，所以在 PDE Specification 对话框中的“Type of PDE”栏中选择“Elliptic”。

分析隧道电场时，静电场是介电常数和空间电荷密度的函数。在求解域中空间内有ρ =0，而在ρ =0 的情况下，介电常数取值不影响静电场分布情况，所以介电常数都取值为1.0。隧道电场PDE 的参数设定如图2-41所示。

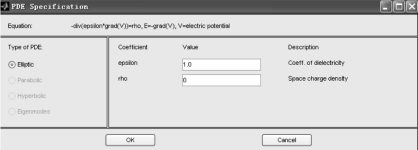
图2-41　隧道电场PDE 参数设定(www.xing528.com)

分析隧道磁场时，静磁场是磁导率μ 和电流密度J 的函数。其中电流密度为

式中，I 为钢轨电流的大小（A），S 为钢轨横截面积（m2）。

根据钢轨电流计算钢轨表面的磁场强度：

式中，I 为钢轨电流的大小（A），P 为钢轨横截面周长（cm）。

由于相对磁导率能更方便地表征磁介质磁性，因此用 rμ 代替μ 以简化求解过程。由实验得到的 μr（ H）函数曲线即可确定相对磁导率，如图2-42所示。

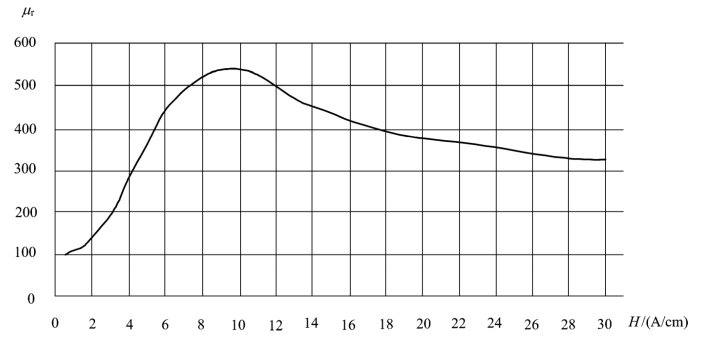
图2-42　钢轨的 μr（ H）函数曲线图

接触轨采用导电性良好的铝平炉软钢制成，单位质量为 51.3 kg/m，横截面积为6 540 mm2，横截面周长为55 cm。走行轨主要成分为铁，选用类型P50，单位质量51.5 kg/m，横截面积为6 570 mm2，横截面周长为62 cm。

磁场接触轨参数：接触轨的电流为3 000 A，电流密度J =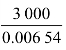=458 715 A/m2，接触轨电流方向为正；磁场强度H =根据图2-42 得接触轨的相对磁导率为240。求解磁场时接触轨PDE 参数设定如图2-43所示。

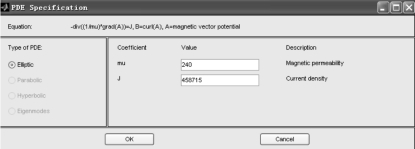
图2-43　隧道磁场接触轨PDE 参数设定

磁场走行轨参数：在计算走行轨电流时应考虑杂散电流的影响，取杂散电流为总电流的10%，所以走行轨电流为3 000 × （1 -10%）/2=1350 A，走行轨电流密度J ==205 479 A/m 2，由于走行轨电流方向和接触轨电流方向相反，所以走行轨的电流密度取-205 479 A/m2。走行轨磁场强度H ==21.8 A/cm，根据图2-42 可得走行轨的相对磁导率为365。求解磁场时走行轨PDE 参数设定如图2-44所示。

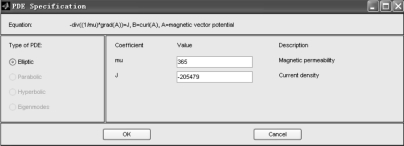
图2-44　隧道磁场走行轨PDE 参数设定

其余区域相对磁导率 rμ 为1，故参数设定J 为0，如图2-45所示。

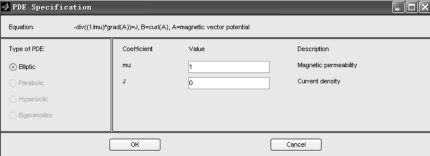
图2-45　隧道磁场剩余区域PDE 参数设定

5.三角形网络部分

在工具栏中单击按钮或在“Mesh”菜单中选择“Initialize mesh”选项，可以进行研究域的三角形网格初始化。在工具栏中单击按钮或在“Mesh”菜单中选择“Refine Mesh”选项，可以对初始网格进行细化。利用细化后的网格进行计算，可以获得具更高精度的解，得到图2-46 和图2-47所示的网格划分。

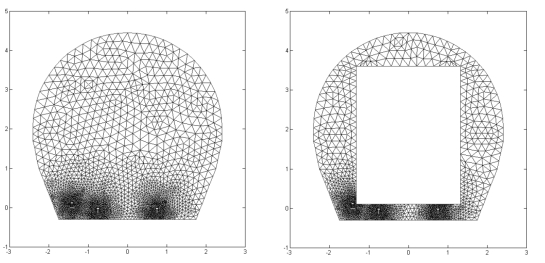
图2-46　隧道电场网格划分

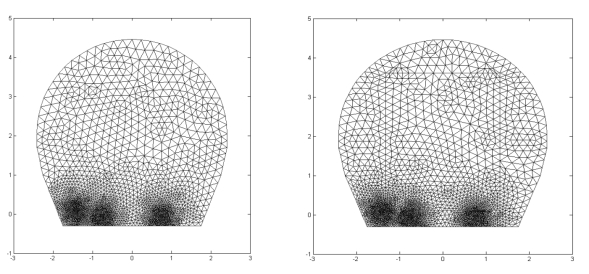
图2-47　隧道磁场网格划分

在“Mesh”菜单中选择“Parameters”选项，打开Mesh Parameters 对话框，如图2-48所示。在该对话框中进行设置，可以明确与网格剖分有关的参数。

图2-48　Mesh Parameters 对话框

6.PDE 求解

在工具条中单击等号按钮或在“Solve”菜单中选择“Solve PDE”选项，可以对前面定义的PDE 问题进行求解。

在“Solve”菜单中单击“Parameters”选项，打开Solve Parameters 对话框，如图2-49所示。在该对话框中进行设置，可以确定求解方法和参数。

7.解的图形表达及仿真结果分析

单击按钮或在“Plot”菜单中选择“Parameters”命令，弹出绘图设置对话框，如图2-50所示，通过设置“Plot”的“Parameters”可以绘出各种要求的分布图。

图2-49　Solve Parameters 对话框

图2-50　Plot Selection 对话框

执行Plot 命令后就得到了在第三轨（750 V）供电方式下，隧道有、无列车电位分布三维图、电位分布俯视图、磁矢位分布三维图、磁矢位分布俯视图和磁感应强度分布三维图。

图2-51、2-52 为隧道无、有列车电位分布三维图，颜色和竖轴都表示电位的大小，颜色越深表示电位越大。由图可知最大电位位于接触轨处，隧道列车的有、无基本不影响接触轨和钢轨的电位大小。图2-53 为隧道无、有列车电位分布俯视图，在Plot Selection对话框中的“Contour plot levels”编辑框中输入50，显示50 条等值线。图中可以清楚地看出电位的分布，其中封闭曲线为等位线，垂直于等位线的红色的箭头为电场强度的方向。等位线越密，电场强度越大，可以看出无论有车、无车，在接触轨处的电场强度最大；但是列车对隧道截面电位的分布影响很大，无列车时电位分布在整个隧道截面，有列车时电位主要集中分布在接触轨附近，由于列车表面电位为0，造成靠近列车表面的等位线出现凹形。

图2-54 为隧道无、有列车静磁矢位分布三维图，颜色和竖轴都表示磁矢位的大小，磁矢位主要分布在导磁材料（接触轨和走行轨）处，最大磁矢位和磁感应强度在接触轨处，磁矢势的方向由电流方向决定。图2-55 为隧道无、有列车磁矢位分布俯视图，在Plot Selection 对话框中的“Contour plot levels”编辑框中输入400，显示400 条等值线，图中可以清楚地看出磁矢位的分布，其中封闭曲线为磁矢位的等值线，等值线越密，磁场强度越大，垂直于等位线的红色的箭头为磁感应强度的方向。隧道有、无列车对磁矢位分布基本无影响。

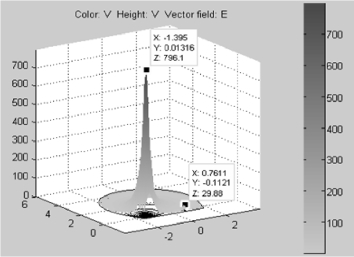
图2-51　隧道无列车电位分布三维图

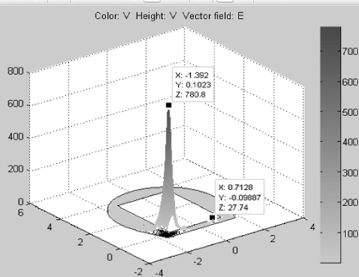
图2-52　隧道有列车电位分布三维图

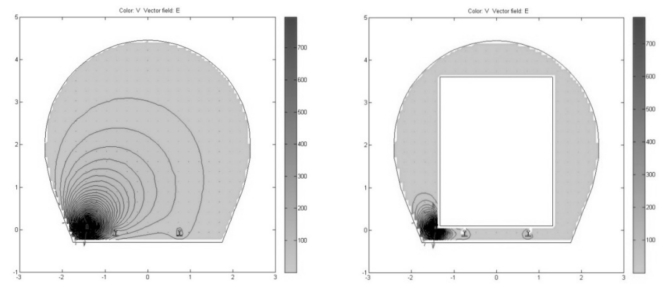
图2-53　隧道无、有列车电位分布俯视图

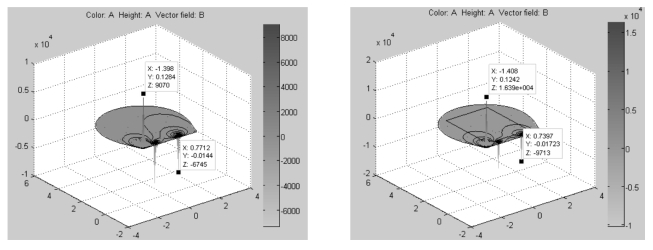
图2-54　隧道静磁矢位分布三维图

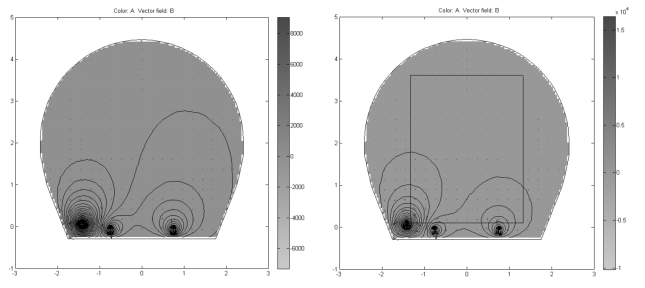
图2-55　隧道无、有列车静磁矢位分布俯视图

图2-56 和2-57 为隧道截面磁感应强度分布三维图，颜色和竖轴都表示磁场强度的大小，磁感应强度主要分布在导磁材料（走行轨）处，虽然接触线、汇流排的电流密度很大，但磁感应强度很小，说明磁感应强度既与相对磁导率有关又与相对磁导率有关。

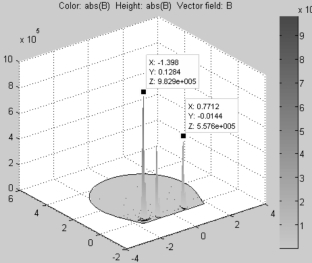
图2-56　隧道无列车磁感应强度三维图

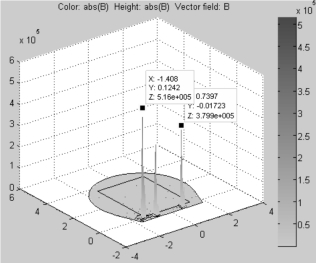
图2-57　隧道有列车磁感应强度三维图