PDEToolbox菜单使用教程

（1）File 菜单（见图2-7）。

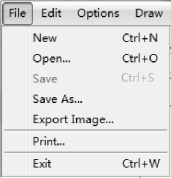
图2-7　File 菜单

New：新建一个几何结构实体模型（Constructive Solid Geometry，简记为CSG），默认未见名为“Untitled”。

Open…：从硬盘装载M 文件。

Save：将在GUI 内完成的成果储存到一个M 文件中。

Save As…：将GUI 内完成的成果储存到另一个M 文件中。

Print…：将PDE 工具箱完成的图形送到打印机内进行硬拷贝。

Exit：退出PDE 工具图形用户界面。

（2）Edit 菜单（见图2-8）。

图2-8　Edit 菜单

Undo：在绘制多边形时退回到上一步操作。

Cut：将已选实体剪切到剪贴板上。

Copy：将已选实体拷贝到剪贴板上。

Paste…：将剪贴板上的实体粘贴到当前几何结构实体模型中。

Clear：删除已选的实体。

Select All：选择当前几何结构实体造型CSG 中的所有实体及其边界和子阈。

（3）Options 菜单（见图2-9）。

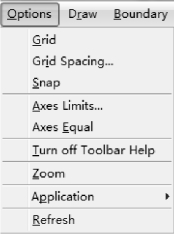
图2-9　Options 菜单

Grid：绘图时打开或关闭栅格。

Grid Spacing…：调整栅格的大小。

Snap：打开或关闭捕捉栅格功能。

Axes Linits…：设置绘图轴的坐标范围。

Axes Equal：打开或关闭绘图方轴。

Turn off Toolbar Help：关闭工具栏按钮的帮助信息。

Zoom：打开或关闭图形缩放功能。

Application：选择应用的模式。

Refresh：重新显示PDE 工具箱中的图形实体。

（4）Draw 菜单（见图2-10）。

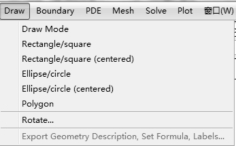
图2-10　Draw 菜单

Draw Mode：进入绘图模式。

Rcctangle/square：以角点方式画矩形/方形（Ctrl+鼠标）。

Rectangle/square（centered）：以中心方式画矩形方形（Ctrl+鼠标）。

Ellipse/circle：以矩形角点方式画椭圆/圆（Ctrl+鼠标）。

Ellipse/circle（centered）：以中心方式画椭圆/圆（Ctrl+鼠标）。

Polygon：画多边形，单击鼠标右键可封闭多边形。

Rotate...：旋转已选的图形。

Export G eometry D escription，Set F ormula，Labels...：将几何描述矩阵gd、公式设置字符sf 和标识空间矩阵ns 输出到主工作空间去。

单击“Draw”菜单中“Rotate...”选项，可打开Rotate 对话框，通过输入旋转的角度，可使选择的物体按输入的角度逆时针旋转，如图2-11。旋转中心的选择如果缺省，则为图形的质心，也可以输入旋转中心坐标。

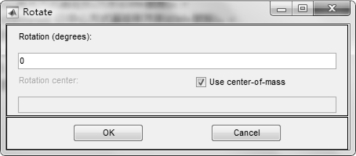
图2-11　Rotate 对话框

（5）Boundary 菜单（见图2-12）。

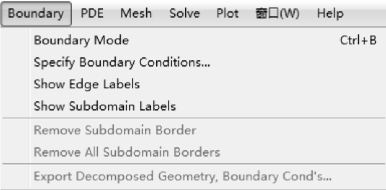
图2-12　Boundary 菜单

Boundary Mode：进入边界模式。

Specify Boundary Conditions...：对于已选的边界输入条件，如果没有选择边界，则边界条件适用于所有的边界。

Show Edge Labels：显示边界区域标识开关，其数据是分解几何矩阵的列数。

Show Subdomain Labels：显示子区域标识开关，其数据是分解几何矩阵中的子域数值。

Remove Subdomain Border：当图形进行布尔运算时，删除已选攻的子域边界。

Remove All Subdomain Border：当图形进行布尔运算时删除所有的子域边界。

Export Decomposed Geometry，Boundary Cond’s...：将分解几何矩阵g、边界条件矩阵b 输出到主工作空间。

选择“Boundary”菜单中“Specify Boundary Conditions...”命令可定义边界条件，如图2-13。在打开的Boundary Condition 对话框中，可对已选的边界输入边界条件。共有如下三种不同的条件类型：

● Neumann 条件。这里边界条件是由方程系数q 和g 确定的，在方程组的情况下，q 是2×2 矩阵，g 是2×1 矢量。

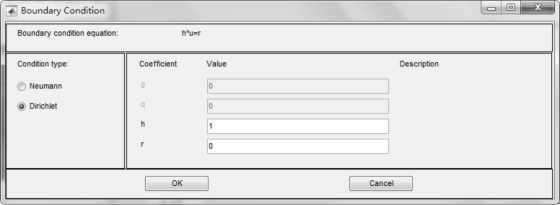
图2-13　定义边界条件对话框

● Dirichlet 条件。u 定义在边界上，边界条件方程是h*u=r，这里h 是可以选择的权因子（通常为1）。在方程组情况下，h 是2×2 矩阵，r 是2×1 矢量。

● 混合边界条件（仅适合于方程组情形）。它是Dirichlet 和Neumann 的混合边界条件，q 是2×2 矩阵，g 是2×1 矢量，h 是1×2 矢量，r 是一个标量。

（6）PDE 菜单（见图2-14）。

图2-14　PDE 菜单

PDE Mode：进入偏微分方程模式。

Show Subdomain Labels：显示子区域标识开关。

PDE Specification...：调整PDE 参数和类型。

Export PDE Coficients....：将当前PDE 参数c，a，f，d 输出到主工作空间，其参数变量为字符类型。

单击“PDE”菜单中“PDE Specification…”选项，可打开如图2-15所示的对话框。从中可选择偏微分方程的类型以及对应用参数作一定的调整。参数的维数决定于偏微分方程的维数。如果选择专业应用模型，那么特殊偏微分方程的参数将代替标准偏微分方程系数。每一个参数c，a，f 或d 皆可作为有效的MATLAB 表达式，以及作为计算三角形单元质量中心的参数值。

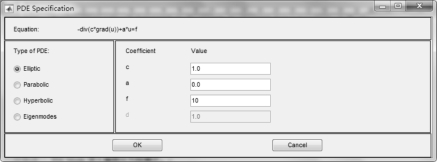
图2-15　PDE Specification 对话框

注意：如果偏微分方程的参数是解u 或者它的导数ux 和uy 的函数，则必须使用非线性求解器；如果偏微分方程参数是时间t 的函数，则需使用抛物型或双曲型偏微分方程。

（7）Mesh 菜单（见图2-16）。

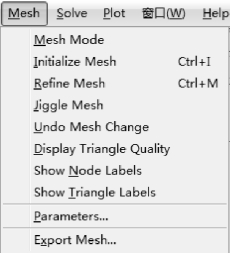
图2-16　Mesh 菜单

Mesh Mode：输入网格模式。

Initialize Mesh：建立和显示初始化三角形网格。(www.xing528.com)

Refine Mesh：加密当前三角形网格。

Jiggle Mesh：优化网格。

Undo Mesh Change：退回上一次网格操作。

Display Triangle Qua lity：用0～1 之间数字化的颜色显示三角形网格的质量，大于0.6 的网格是可接受的。

Show Node Labels：显示网格节点标识开关、节点标识数据是点矩阵p 的列。

Show Triangle Labels：显示三角形网格标识开关，三角形网格标识。数据是三角形矩阵t 的列。

Parameters...：修改网格生成参数。

Export Mesh...：输出节点矩阵p、边界矩阵e 和三角形矩阵t 到主工作空间。

（8）Solve 菜单（见图2-17）。

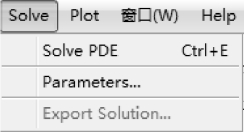
图2-17　Solve 菜单

Solve PDE：对当前的几何结构实体CSG、三角形网格和图形解偏微分方程。

Parameters...：调整解PDE 的参数。

Export Solution...：输出PDE 的解矢量u。如果可行，将计算的特征值I 输出到主工作空间。

单击“Solve”菜单中“Paramets...”选项，打开Solve Parameters 对话框，从中可输入解方程的参数。每组参数的选择取决于PDE 的类型。

① 对于椭圆型偏微分方程，在缺省方式下，不需要专门定义解方程的参数。解椭圆方程采用基本方程求解器assempde。在自适应网格生成和adaptmesh 之间进行选择。对于自适应网格方式，如图2-18所示。

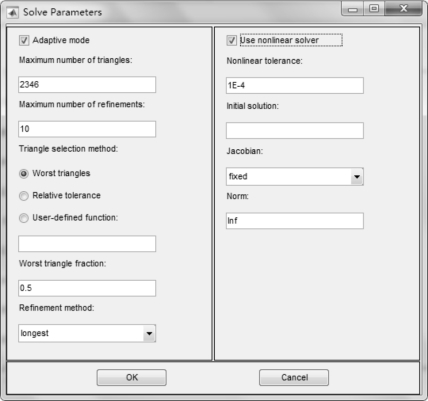
图2-18　Solve Parameters 对话框

② 对于抛物型偏微分方程（Parabolic PDEs），解抛物型的参数如图2-19所示。

图2-19　抛物型偏微分方程的参数

Time：求解抛物型偏微分方程的MATLAB 时间矢量。相关时间间隔依赖于问题的动态状况。例如：输入“0：10”或“logspace（-2，0，20）”等。

u（t0）：对于抛物型偏微分方程的初始值是u（n）。初始值可以是一个常数或者是当前网格的节点值的列向量。

Relative tolerance：相对容差。对于常微分方程ODE 的求解器的相对容差参数，是用来求解拋物型偏微分方程有关时间部分。

Absolute tolerance：绝对容差。对于常微分方程ODE 的求解器的绝对容差参数，是用来求解拋物型偏微分方程有关时间部分。

③ 对于双曲型偏微分方程（Hyperbolic PDEs）， 解双曲型的参数如图2-20所示。

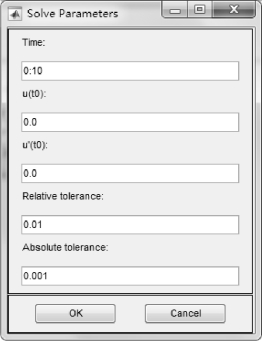
图2-20　双曲型偏微分方程的参数

Time（时间）：求解双曲型偏微分方程的MATLAB 时间矢量。相关时间间隔依赖于问题的动态状况。

u（t0）：对于双曲型偏微分方程的初始值是u（t0）。初始值可以是一个常数或者是当前网格的节点值的列向量。

′u（t0）：对于双曲型偏微分方程的初始值是u′（t0），可使用与u（t0）相同的格式。

Relative tolerance（相对容差）：对于常微分方程ODE 的求解器的相对容差参数，是用来求解双曲型偏微分方程有关时间部分。

Absolute tolerance（绝对容差）：对于常微分方程ODE 的求解器的绝对容差参数，是用来求解双曲型偏微分方程有关时间部分。

（9）Plot 菜单（见图2-21）。

图2-21　Plot 菜单

Plot Solution：显示图形解。

Parameters...：打开绘图方式对话框。

Export Movie...：如果动画被录制了，则动画矩阵M 将输出到主工作空间。

单击“Plot”菜单中“Parametes...”选项，可打开Plot Selection 对话框，如图2-22所示。其中含有控制绘图和可视化选项部分。

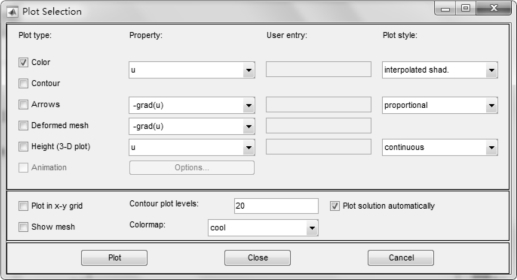
图2-22　Plot Selection 对话框

Color（颜色）：用于着色曲面标量属性的可视化。

Contour（等值线）：用于等值线标量属性的可视化。当绘图类型（颜色和等值线）被检查后，等值线可提高颜色的可视化，等值线被两成黑色。

Arrows（箭头）：用箭头表示矢量属性的可视化。

Deformed mesh（变形网格）：用向量属性表示变形网格的可视化。变形会自动地控制在问题区域的10%。这种绘图类型基本上要把结构力学中的x 和y 位移（u 和v）显示出来。如果没有其他的绘图类型选取，那么变形三角形网格会被显示出来。

Height（3-D plot）（三维图形）：分别用不同图形窗口进行三维图形（3-D plot）标量属性的可视化。如果颜色和等值线的绘图类型没有选取，则三维图形（3-D plot）绘出的仅仅是网格图，当然也可以在三维图形（3-D plot）中同时用颜色和（或）等值线绘出其他标量属性。

Animation（动画）：在抛物型和双曲型问题中依赖于时间解的动画。如果选取了这个选项，方程解就被记录下来，然后用movie 函数可在不同的图形窗口中做动画演示。

Property（属性）：用于画图时选用相应的绘图类型。

第一个弹出菜单用于控制颜色或等值线的显示属性。其中

U：方程的解。

abs（grad（u））：每个三角形的中心的Vu 的绝对值。

abs（c*grad（u））：每个三角形的中心的c.Vu 的绝对值。

user entry：MATLAB 表达式，返回一个定义在当前三角形网格的节点或者三角形上的数据矢量。选取User entry 项，可以将表达式输入到右边的User entry 的编辑框中。

u 的导数是ux 和uy。第二和第三个弹出菜单，通过使用箭头和变形网格可视化图形表示矢量值属性。其中

-grad（1）：u 的负梯度，即-Vu。

-c*grad（u）：c 乘以u 的负梯度，即 -c u∇ 。

user entry：MATLAB 表达式[px；py]可返回一个2xn 维定义当前三角形网格数据的矩阵。

解u，其导数ux 和uy，c u∇ 的x 和y 分量，皆适用于局部空间。三角形中心的值是由节点插值得到的。可以在右边User entry 中对属性弹出式菜单进行赋值。

对于方程组情形，若使用颜色、等值线或三维绘图等可视化属性是u，v，abs（u，v）和用户输入框。

若使用箭头或变形网格，可选择（u，v）或用户框。对于结构力学中的应用来说，u和v 分别是x 和y 方向的位移。

User entry（位于第三列）：含有4 个编辑框，可供用户输入自己的表达式。只有当用户在编辑窗左边的弹出菜单选择了User entry 项，才可输入属性。

Plot style（位于第四列）：绘图方式含有三个弹出菜单，可分别用作对颜色、箭头及三维绘图的属性控制。

对于箭头（Arrows）绘制有两种方式可选择：

Proportional：箭头的长度与设置的有关属性大小相对应。

Normalized：所有的箭头的长度都是相等的，这对于只想了解矢量场的方向是很有用的，即使区域很小时，矢量的方向也清晰可见。

在对话框底部有许多辅助绘图控制选择项如下。

Plot in x-y grid：如果选择了此项，图形解将原来的三角形网格转变成矩形x-y 网格。这对于动画来说是非常有用的，因为四边形网格可有效地加速动画片存储过程。

Show mesh：在曲面图中，如果选择此项，网格被画成黑色；如果缺省，网格消隐。

Contour plot levels：等值线条数，比如，输入15 或20，系统会按此数目画出等值线，缺省值为20。

Colormap：使用Colormap 弹出菜单，可以选择不同的色图，如cool，gray，bone，pink，copper，bot，jet，hsv 和prism。

Plot solution automatically：如果关闭此项，则PDE Toolbox 不会立刻显示图解。然而，新解仍然可以用这个对话框画出来。

至此，Plot selection 对话框设置完毕，若点击“Plot”按钮，则按当前图形设置，其解立刻被绘出；如果当前没有偏微分方程，则首先解方程，有了解以后再绘图。

若点击“Done”按钮，对话框则会关闭。当前的设置将被储存，没有新图形产生。

若点击“Cancel”按钮，对话框则会关闭，设置不会改变。