工程电磁场仿真:麦克斯韦方程组应用

电磁场数值分析是根据电磁场的基本特性，即基于麦克斯韦方程组：首先，建立逼近实际工程电磁场的数学模型；然后，采用相应的数值计算方法，经离散化处理，把连续型数学模型转化为离散型数学模型—— 由离散数值构成的联立代数方程组（离散方程组），应用有效的代数方程组解法，计算出数学模型的离散解（即场量的数值解）；最后，在所得该电磁场场量（含势函数）离散解的基础上求出所需的场域中任意点处的场强、任意区域的能量、损耗分布，以及各类电磁参数与性能指标等，以达到对给定的工程电磁场正问题进行理论分析、工程判断乃至优化设计等目的。

麦克斯韦方程组是麦克斯韦提出的可用于所有宏观电磁现象的理论模型，它是电磁场理论的基础，主要由安培环路定律、法拉第电磁感应定律、高斯电通定律和高斯磁通定律（磁通连续性定律）组成。

磁场中磁场强度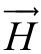在任意闭合路径上的积分和穿过其所围成曲面S 内的电流之和相等，称为安培环路定律。积分表示为

式中，Γ 是S 的边界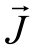，是电流密度矢量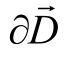，/ ∂t是电流密度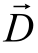，是电通密度。

在闭合回路中，感应电场的环量与回路中的磁通量随时间的变化成正比。称为法拉第电磁感应定律。积分式为

式中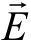，为电场强度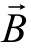，为磁感应强度。

电场中穿过任意闭合曲面的电通量与该曲面围聚的电荷量相等，称为高斯电通定律。积分表示为

式中，V 是S 围成的体积，ρ 是电荷体密度。

在磁场中任意闭合曲面的磁通量恒为零，磁通量是磁通矢量对这个曲面的积分，称为高斯磁通定律。积分表示为(www.xing528.com)

式（1-4）表明磁场为无源场。

引入位移电流假说，方程组可以表示成对应的微分形式：

添加介质特征，可写出电磁场的辅助方程组：

式（1-6）中，ε μ、 和σ 分别表示介电常数、磁导率和电导率。

在变化的电磁场中，一般需对方程组做简化以便于求解，为把电场矢量和磁场矢量分离开来，定义两个物理量，即矢量磁位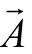（ ）和标量电势（φ）；如下公式：

因矢量磁位和标量电势满足法拉第电磁感应定律和高斯磁通定律，结合安培环路定律和高斯磁通定律推导出磁场偏微分方程和电场偏微分方程：

式中，∇ 2表示拉普拉斯算子：