微机原理：计算机的定点数和浮点数

人们常用的数据一般有三种：纯整数（如二进制数1010B）、纯小数（如二进制数0.1001B）及既含整数又含小数的数（如二进制数11101.0011B）。在计算机中，表示这三种数有两种方法：定点表示法和浮点表示法。

计算机中数的小数点位置固定的表示法称为定点表示法，用定点表示法表示的数称为定点数。

计算机中数的小数点位置不固定的表示法称为浮点表示法，用浮点表示法表示的数称为浮点数。

值得注意的是：小数点在计算机中是不表示出来的，也就是说，它不占据一个二进制位，而是隐含在用户规定的位置上。

原则上讲，上述三种数用任何一种表示法都可以。但实际上，纯整数和纯小数用定点表示法比较方便；而既含整数又含小数的数用浮点表示法时，比较实用且便于运算。

1.定点纯整数

用n位二进制表示一个数，其中最高位（B_n−1）表示数的符号，小数点固定在最低位（B₀）的最右边，这样的数称为定点纯整数，如图1-3所示。

图1-3 定点纯整数的表示

正如在1.1.3节中所介绍的，计算机中的有符号数一般用补码形式的定点纯整数表示。n位补码定点纯整数的表示范围为−2ⁿ⁻¹～2ⁿ⁻¹−1。例如：8位（n=8）二进制补码表示的定点纯整数的范围是−128～+127。

2.定点纯小数

用n位二进制表示一个数，其中最高位（B_n−1）表示数的符号，小数点固定在符号位（B_n−1）之后，最高数据位（B_n−2）之前，这样的数称为定点纯小数，如图1-4所示。

图1-4 定点纯小数的表示

定点整数或定点小数所允许表示的数值范围有限，运算精度较低，但采用定点运算时对硬件要求较简单。

3.浮点数

对于一些绝对值很大的数，或要求表示的数值范围很广的数，经常采用浮点表示法。(www.xing528.com)

如前所述，一个二进制数N可以表示为N=S⋅2^P。

其中S称为浮点数的尾数，P称为阶码，S规定为定点小数，P为定点整数。2为阶码的基数。在计算机中浮点数通常表示为如图1-5所示的格式。

图1-5 浮点数格式

由图1-5可见，要表示一个浮点数，一是要给出尾数S，尾数S通常用定点小数形式表示，它决定了浮点数的表示精度，即给出有效数字的位数；二是要给出阶码P，通常用整数形式表示，它指出的是小数点在数据中的位置，决定了浮点数的表示范围。尾符Sr是尾数的符号位，尾符Sr的正、负表示整个数的正、负，即尾符Sr决定了整个数的正、负，而阶码Pr是阶码的符号位，阶码Pr的正、负表示尾数S的小数点按照阶码Pr的值左移（负）或者右移（正）。

一般阶码P用补码表示，便于指数加减运算。尾数可以取补码或原码，但常用原码表示，因为原码便于乘除运算，而进行加减运算时，也方便转换成补码再进行运算。

若一个浮点数的阶码P有m位（不包括阶符Pr），尾数S有K位（不包括尾符Sr），则可表示数的最大绝对值是：阶符Pr为正、阶码P和尾数S全为“l”时，即

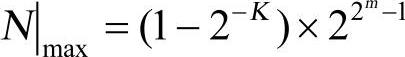
而可表示数的最小绝对值是：阶符Pr为负，阶码P为全“1”，尾数S最低位为“1”，其余为“0”时，即

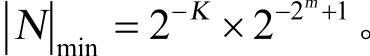
用浮点数进行运算，可减小计算精度上的损失，但由于浮点数的小数点是不固定的，在运算前需要使小数点对位。若两数的“阶”不同，则在运算前首先要“对阶”，且按大的阶码值对阶，否则可能丢失数字的有效位而引起误差。

一般浮点数都以“规格化”形式表示，若是原码尾数，最高尾数位为“1”是规格化形式；若是补码尾数，则正数的最高尾数位为“1”、负数的最高尾数位为“0”才是规格化数，即尾数的最高位与尾符Sr必须相反。

采用“规格化”形式表示浮点数，可以保留最多的有效数字，提高运算精度。

例如：数0.000101×2⁵的规格化表示为0.101×2²。

在浮点数表示中，当一个数的阶码大于机器所能表示的最大阶码时，产生“上溢”，转入“溢出中断”处理；当一个数的阶码小于机器所能表示的最小阶码或尾数为0时，则产生“下溢”，下溢时机器一般将此当做“机器零”来处理。

可以看出，要扩大数的表示范围，应增加阶码的位数；而要增加精度，就需要增加尾数的位数。对同样字长，浮点数比定点数表示的数值范围要大许多，但浮点数运算操作复杂。浮点数产生溢出实质上是阶码溢出。