微机原理：带符号数表示

计算机中使用的数据分为无符号数和有符号数两种。上面几节阐述的二进制数，是一种无符号数的表示，例如：8位无符号数表示的范围为00H～FFH（0～255）。但是在机器中，有符号的数据有正、负之分，那么符号是怎样表示的呢？通常一个数的最高位为符号位，符号位为“0”表示正数，符号位为“1”表示负数，其余为数值。若字长为8位，即D₇为符号位，D₆～D₀为数值位。符号位D₇为“0”表示正数，为“1”表示负数。8位有符号数T₁的表示如图1-1所示。

图1-18 位有符号数的表示

若字长为16位，D₁₅为符号位，D₁₄～D₀位为数值位，16位有符号数T₂表示如图1-2所示。

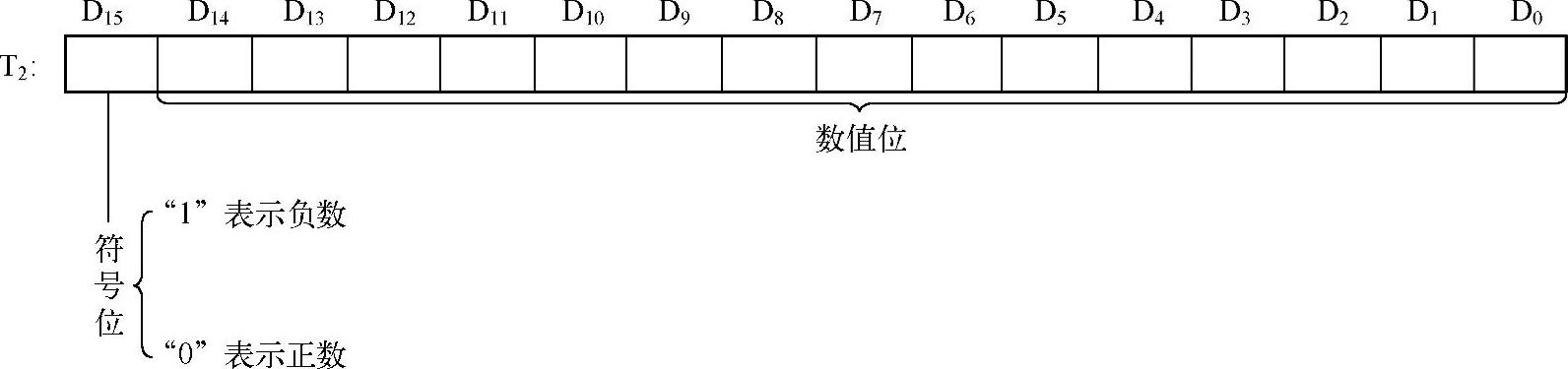
图1-2 16位有符号数的表示

字长是衡量计算机运算精度的指标，在计算机中完成一次运算和处理所对应的一组二进制数的位数称为计算机的字长。字长越长，计算处理的二进制有效位数越多，计算的精度越高。在机器中，用二进制数表示有符号数，用最高位表示符号，其余的为数值位，这样一组连同符号一起编码化的二进制数称为机器数，机器数所代表的数值的大小称为机器数的真值。

数据在计算机内采用符号化处理后，机器可表示并识别带符号的数据。为了改进运算方法，简化控制电路，人们研究出多种有符号数的编码方式，最常用的有三种表示方法，即原码、反码和补码。

数X的原码记作[X]_原，反码记作[X]_反，补码记作[X]_补。

1.原码

在机器数中最高位为符号位，符号位为“0”表示正数，符号位为“1”表示负数，其余为该数的绝对值，这种表示方法就称为原码。即仅将符号位数字化表示为0或1，数的绝对值与符号一起编码。

原码的特点：

①最高位为符号位，正数为0，负数为1。

②8位二进制原码表示数的范围是−127～+127；16位二进制原码表示数的范围是−32767～+32767。

③0的原码有两种表示方法，即+0和−0，设字长为8位：

[+0]_原=00000000B；[−0]_原=10000000B

采用原码表示法时，编码简单直观，与真值转换方便。但也带来一些麻烦，一是引起机器中零的表示不唯一，0有二义性，给机器判零带来麻烦，必须在设计时约定好机器采用正零或负零；二是不便于进行加减运算。用原码进行四则运算时，符号位需单独处理，而且原码加减运算规则复杂。例如，对有符号数的加法规则是：若两个数同号，两数绝对值相加，结果冠以共同的符号；若两个数异号，两数绝对值相减，结果冠以绝对值大的数值的符号，而减法又有一套规则。故原码表示法一般不用于加减运算。

2.反码

正数的反码与原码相同，负数反码等于原码除符号位保持为“1”外，其余各位按位取反。

反码的特点：

①反码表示法中，最高位仍为符号位，正数为0，负数为1。

②“0”有两种表示方法：

当n=8时：[+0]_反=00000000B；[−0]_反=11111111B

③8位二进制反码表示数的范围是−127～+127；16位二进制反码表示数的范围是−32767～+32767。

④正数的反码与原码相同，负数反码符号位为“l”不变，其数值部分按位取反得到该数据的反码。

3.补码(www.xing528.com)

正数的补码表示与原码相同，即最高位为符号位，其余位为数值位；负数的补码等于它的反码加1，即在其反码的最低位加1就为该数的补码。

补码的特点：

①补码表示法中，最高位仍为符号位，正数为0，负数为1。

②“0”仅有一种表示方法，即[+0]_补=[−0]_补。

③8位二进制补码表示数的范围是−128～+127。16位二进制补码表示数的范围是−32768～+32767。

④对于8位二进制数10000000B，在补码中定义为[−128]，在原码中定义为[−0]，在反码中定义为[−127]；16位二进制数1000000000000000B，在16位的补码中定义为[−32768]。

在微型计算机中，所有带符号的数据都是用补码表示。一个数据是带符号数还是不带符号数，事先是规范好的，是已知的。

8位二进制数的原码、反码和补码见表1-1。

表1-1 原码、反码和补码

4.数的补码与真值

（1）正数补码与真值的关系

如前面所述，正数的原码[X]_原等于正数的补码[X]_补，即[X]_补=[X]_原，所以正数补码的真值X=[X]_补。

（2）负数补码与真值的关系

负数补码求一次该负数补码的反码，然后+1，即可得到补码对应真值的绝对值，其符号位也参与求反运算。 即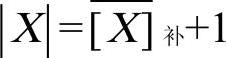；其中表示对补码进行求反运算。

例1-1 [X]_补=10000010B，求[X]_真值。

解：因为该二进制补码符号位为“1”，该补码对应的真值是负数，则

由于[X]_补的符号位为1，则[X]_真=-01111110=-126

例1-2 求8位补码01111111B和10000001B的真值。

解：（1）因为[X]_补=01111111B，符号位为“0”，该补码对应的真值是正数，

则[X]_真=[X]_补=01111111B=+127D

（2）因为10000001B的符号位为“1”，该补码对应的真值是负数，其绝对值为

则[X]_真=-01111111B=-127D