【摘要】：例8.10（全国大学生2013年决赛题）设函数f（u，v）具有连续偏导数，且满足（u，v）+（u，v）=uv，求y（x）=e-2xf（x，x）所满足的一阶微分方程，并求其通解.解析由于y′（x）=-2e-2xf（x，x）+e-2x（（x，x）·1+（x，x）·1）=-2y（x）+x2e-2x所以y（x）所满足的一阶微分方程是y′+2y=x2e-2x，其通解为例8.11（江苏省2000年竞赛题）
例8.10（全国大学生2013年决赛题） 设函数f（u，v）具有连续偏导数，且满足
（u，v）+
（u，v）=uv，求y（x）=e-2xf（x，x）所满足的一阶微分方程，并求其通解.
解析 由于
y′（x）=-2e-2xf（x，x）+e-2x（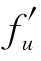
（x，x）·1+
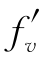（x，x）·1）
=-2y（x）+x2e-2x
所以y（x）所满足的一阶微分方程是y′+2y=x2e-2x，其通解为
例8.11（江苏省2000年竞赛题） 设函数f（x）在（-∞，+∞）上连续，且满足
求f（x）.
代入原式得
两边求导数得(www.xing528.com)
f′（t）=4πt3f（t）+4t3，f（0）=0
此为一阶线性微分方程，其通解为
由f（0）=0得C=
于是f（x）=
例8.12（江苏省1994年竞赛题） 设f（x）为定义在［0，+∞）上的连续函数，且满足
求f（1）.
解析 首先应用球坐标计算三重积分，记Ω：x2+y2+z2≤t2，则
代入原式得
则f（0）=0.上式两边求导得f′（t）=4πt2f（t）+3t2，此为一阶线性方程，通解为
由f（0）=0得C=
于是f（t）=
，故f（1）=
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
