2016高等数学竞赛题解析教程：二阶微分方程

1）用降阶法解特殊的二阶微分方程

（1）y″=f（x）：积分两次即得通解

（2）y″=f（x，y′）：令y′=u，则原方程化为一阶方程u′=f（x，u）.

（3）y″=f（y，y′）：令y′=u，y″=则原方程化为一阶方程

2）二阶线性微分方程通解的结构

二阶线性微分方程的标准形式为

y″+p（x）y′+q（x）y=f（x）　（1）

y″+p（x）y′+q（x）y=0　（2）

称方程（2）为方程（1）所对应的齐次方程，称方程（2）的通解为方程（1）的余函数.

定理1　设y1（x）与y2（x）是方程（2）的两个线性无关解，则方程（2）的通解为

y=c1y1（x）+c2y2（x）

这里c1与c2为两个任意常数.

定理2　设y1（x）与y2（x）是方程（2）的两个线线无关解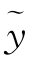，（x）是方程（1）的任一特解，则方程（1）的通解为

y=c1y1（x）+c2y2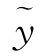（x）+（x）

定理3　设方程（1）中f（x）=f1（x）+f2（x）.若方程

y″+p（x）y′+q（x）y=f1（x）

y″+p（x）y′+q（x）y=f2（x）

分别有特解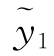（x）与（x），则方程（1）有特解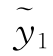（x）+（x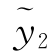）.(www.xing528.com)

定理4　方程（1）的任意两个特解的差是方程（2）的一个特解；方程（1）的任意两个特解的平均值仍是方程（1）的一个特解.

3）二阶常系数线性齐次方程的通解公式：二阶常系数线性齐次方程

y″+py′+qy=0　（3）

的特征方程为

λ2+pλ+q=0　（4）

当p2-4q＞0时，方程（4）有两个相异实根λ1，λ2（λ1≠λ2），此时方程（3）的通解为

当p2-4q=0时，方程（4）有两个相等的实根λ1，λ2（λ1=λ2），此时方程（3）的通解为

当p2-4q＜0时，方程（4）有两个共轭复根λ1=α+βi，λ2=α-βi，其中α=，此时方程（3）的通解为

y=eαx（c1cosβx+c2sinβx）

4）二阶常系数线性非齐次方程的特解

设方程

y″+py+qy=f（x）　（5）

当右端的函数f（x）为指数函数eαx、多项式Pn（x）、三角函数acosβx+bsinβx或者它们的乘积时，可用待定系数法求方程（5）的一个特解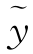（x）.这里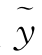（x）与f（x）有相同的形式，或在此相同形式前乘以xk（k=0，1，2）.具体地说，当α或α+βi不是特征根时，k=0；当λ=0不是特征根时，k=0；当α或α+βi是单特征根时，k=1；当λ=0是单特征根时，k=1；当α是二重特征根时，k=2.

5）欧拉方程：二阶欧拉方程的标准形式是

x2y″+pxy′+qy=f（x）　（6）

作自变量的变换，令x=et，则

代入方程（6）化为常系数线性方程