【摘要】:例7.55(江苏省1991年竞赛题)函数f(x)=ln(1-x-2x2)关于x的幂级数展开式为________,该幂级数的收敛域为________.解析因为ln(1-u)=--1≤u<1,所以收敛域为-1<x≤1与-1≤2x<1的交集,即例7.56(江苏省2000年竞赛题)将f(x)=展开为x的幂级数,并指明收敛域.解析首先求f′(x)的幂级数展开式,有这里|x|<1.逐项求积分得因f(0
例7.55(江苏省1991年竞赛题) 函数f(x)=ln(1-x-2x2)关于x的幂级数展开式为________,该幂级数的收敛域为________.
解析 因为ln(1-u)=-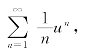 -1≤u<1,所以
-1≤u<1,所以
收敛域为-1<x≤1与-1≤2x<1的交集,即![]()
例7.56(江苏省2000年竞赛题) 将f(x)=![]() 展开为x的幂级数,并指明收敛域.
展开为x的幂级数,并指明收敛域.
解析 首先求f′(x)的幂级数展开式,有
这里|x|<1.逐项求积分得
因f(0)=arctan1=![]() 所以
所以
例7.57(南京大学1993年竞赛题) 函数f(x)=![]() 关于x的幂级数展开式中x3的系数为________,收敛半径为_________.
关于x的幂级数展开式中x3的系数为________,收敛半径为_________.
解析 由于|x|<3时
逐项积分得
于是x3的系数(n=1时)为![]() 收敛半径为3.
收敛半径为3.
例7.58(南京大学1995年竞赛题) 试将函数![]() 展为马克劳林级数,并写出其收敛域.
展为马克劳林级数,并写出其收敛域.
解析 因为
下面分别将g(x)=![]() 展为幂级数.因为
展为幂级数.因为
两边求导得
又因为(https://www.xing528.com)
所以f(x)的幂级数展式为
其收敛域为|x|<3与|x|<![]() 的交集,即|x|<
的交集,即|x|<![]()
例7.59(江苏省2008年竞赛题) 求f(x)=![]() 关于x的幂级数展开式,指出其收敛域.
关于x的幂级数展开式,指出其收敛域.
解析 因为f(x)=![]() 又
又
令g(x)=![]() 则
则
即g(x)=![]() 故
故
例7.60(江苏省2008年竞赛题) 求f(x)=![]() 关于x的幂级数展开式,指出其收敛域.
关于x的幂级数展开式,指出其收敛域.
解析 因f(x)=![]() 又
又
令g(x)=![]() 则
则
令h(x)=![]() 则
则
故
例7.61(精选题) 将幂级数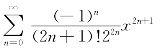 的和函数展为x-1的幂级数.
的和函数展为x-1的幂级数.
解析 应用函数sinx的马克劳林展式得原级数的和函数为
令x-1=t,应用sinx与cosx的马克劳林展式,则
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




