【摘要】：例7.47计算解析由于k！［1+（k+1）+（k+1）（k+2）］=k！
例7.47（北京化工大学1991年竞赛题） 计算
解析 由于
k！+（k+1）！+（k+2）！=k！［1+（k+1）+（k+1）（k+2）］=k！（k+2）2
所以
考虑幂级数
则f′（x）=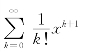
=
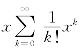=xex，于是
令x=1，得
例7.48（江苏省2004年竞赛题） 
=_____________.
解析 首先求幂级数
的和函数，有
令x=
得
故原式=
=2（1-ln2）.
例7.49（江苏省2002年竞赛题） 求
的和.
解析 首先考虑幂级数为
逐项积分得
令g（x）=
（|x|＜1），逐项积分得
两边求导得
于是
两边求导得
所以
例7.50（莫斯科电子技术学院1977年竞赛题） 求级数
的和.
解析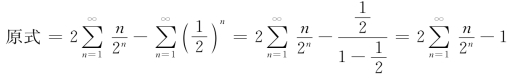 
令f（x）=
|x|＜1，逐项求积分得
两边求导得f（x）=
|x|＜1.令x=
得
故原式=4-1=3.(https://www.xing528.com)
解析 令
两次逐项求导得
（1）式两边积分得
（2）式两边积分得
于是
例7.52（江苏省2012年竞赛题） 求级数
的和
解析 原式=
现令
于是
因此
又
故原式=8-
例7.53（莫斯科全苏大学生1975年竞赛题） 试求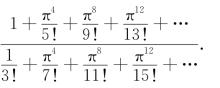
解析 记p=
则
由于sinx的幂级数展开式为
所以πp-π3q=sinπ=0，即原式=
=π2.
例7.54（莫斯科钢铁与合金学院1977年竞赛题） 证明：当p≥1时，有
解析 令xn=
于是
由拉格朗日中值定理，存在θ∈（0，1），使得
于是
又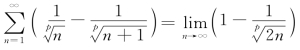
=1，因此
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
