例7.1(莫斯科自动化学院1977年竞赛题) 讨论![]() 的敛散性,其中{xn}是方程x=tanx的正根按递增顺序编号而得的序列.
的敛散性,其中{xn}是方程x=tanx的正根按递增顺序编号而得的序列.
解析 由x>0与tanx的周期性可知
于是xn>-![]() +nπ>n,因此
+nπ>n,因此![]() 由比较判别法知
由比较判别法知![]() 收敛.
收敛.
例7.2(浙江省2002年竞赛题) 设{an},{bn}为满足![]() 的两个实数列,已知an>0(n≥1),且
的两个实数列,已知an>0(n≥1),且![]() 收敛,证明:
收敛,证明:![]() 也收敛.
也收敛.
解析 由于![]() 收敛,所以
收敛,所以![]() =0.因an>0,且
=0.因an>0,且
故bn>0,且![]() 于是级数
于是级数![]() 收敛.
收敛.
例7.3(北京市1997年竞赛题) 已知{un}是单调增加的正数列,试证明:级数![]() 收敛的充分必要条件是数列{un}有界.
收敛的充分必要条件是数列{un}有界.
解析 先证充分性.令an=![]() 因{un}单调增,所以an≥0,且an≤
因{un}单调增,所以an≥0,且an≤![]() 由于
由于
因{un}单调增并有界,故数列{un}收敛.设![]() =A,则
=A,则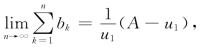 故级数
故级数![]() 收敛,由比较判别法得
收敛,由比较判别法得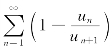 收敛.
收敛.
再证必要性.若{un}无界,则对于任意的k∈N,均存在n>k,使un>3uk.令ai=![]() 则
则
根据柯西收敛准则得数列{Sn}发散,则原级数发散.导出矛盾,故假设不成立,因此数列{un}有界.
例7.4(南京大学1995年竞赛题) 求![]()
解析 令an=![]() 考虑级数
考虑级数![]() ,因为an>0,且
,因为an>0,且
据比值判别法知![]() 收敛,而级数收敛的必要条件是an→0(n→∞),故原式=0.
收敛,而级数收敛的必要条件是an→0(n→∞),故原式=0.
解析 已知a1=1>0,a2=2>0,a2-a1=1>0,归纳设an>0,an-an-1>0,则
an+1-an=2an-an-1=(an-an-1)+an>0
即an+1>an>0,所以数列{an}严格增.且∀n∈N,an>0,由
3an=an-1+an+1<2an+1
由于级数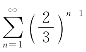 收敛,应用比较判别法得
收敛,应用比较判别法得![]() 收敛.
收敛.
例7.6(全国大学生2013年初赛题) 判别级数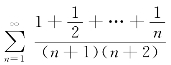 的敛散性;若收敛,求其和.
的敛散性;若收敛,求其和.
解析 由于
故an=![]() 当n充分大时,因为1+lnn<
当n充分大时,因为1+lnn<![]() 所以
所以
而级数![]() 收敛,应用比较判别法,即得原级数收敛.
收敛,应用比较判别法,即得原级数收敛.
考虑原级数的部分和
因n→∞时![]() ,故Sn→1.即原级数的和为1.
,故Sn→1.即原级数的和为1.
例7.7(全国大学生2010年初赛题) 设an>0(n=1,2,…),![]() ,证明:
,证明:
(1)当α>1时,级数![]() 收敛;
收敛;
(2)当α≤1且Sn→+∞(n→∞)时,级数![]() 发散.
发散.
解析 (1)当α>1时,设f(x)=x1-α,在区间[Sn-1,Sn]上应用拉格朗日中值定理,必∃ξ∈(Sn-1,Sn),使得
由此式可得
设正项级数![]() 的部分和为σn,由于
的部分和为σn,由于
所以级数![]() 收敛,应用比较判别法即得级数
收敛,应用比较判别法即得级数 收敛.
收敛.
(2)当α=1时,设g(x)=lnx,在区间[Sn-1,Sn]上应用拉格朗日中值定理,必∃η∈(Sn-1,Sn),使得
由此式可得
设正项级数![]() 的部分和为σn,由于
的部分和为σn,由于
所以级数![]() 发散.又由于
发散.又由于
![]() (这里设数列{an}收敛)
(这里设数列{an}收敛)
所以级数![]() 发散,应用比较判别法,即得级数
发散,应用比较判别法,即得级数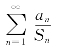 发散.
发散.
当α<1时,不妨设Sn>1,因![]() 应用比较判别法,即得级数
应用比较判别法,即得级数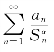 发散.
发散.
例7.8(浙江省2011年竞赛题) 已知正项级数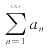 收敛,试证明级数
收敛,试证明级数![]() 收敛.
收敛.
解析 对于正项级数![]() 的部分和
的部分和
应用不等式k!≥![]() (k∈N*)与几何平均数小于等于算术平均数,有
(k∈N*)与几何平均数小于等于算术平均数,有
由于
所以
由于收敛级数![]() 的部分和有界,所以级数
的部分和有界,所以级数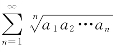 的部分和有界,于是级数
的部分和有界,于是级数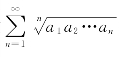 收敛.
收敛.
例7.9(莫斯科动力学院1975年竞赛题) 对于级数![]() (其中an>0),若
(其中an>0),若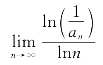 =λ,求证:当λ>1时级数
=λ,求证:当λ>1时级数![]() 收敛;当λ<1时级数
收敛;当λ<1时级数![]() 发散.
发散.
解析 (1)当λ>1时,取p:1<p<λ,由极限性质,∃N∈N,当n≥N时,有
而p>1时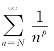 收敛,所以
收敛,所以![]() 收敛,因而
收敛,因而![]() 收敛.
收敛.
(2)当λ<1时,取p:λ<p<1,由极限性质,∃N∈N,当n≥N时,有
而p<1时![]() 发散,所以
发散,所以![]() 发散,因而
发散,因而![]() 发散.
发散.
例7.10(全国大学生2012年初赛题) 设![]() 为正项级数.
为正项级数.
(1)若![]() ,证明
,证明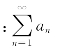 收敛;
收敛;
(2)若![]() ,且
,且![]() 发散,证明
发散,证明![]() 发散.
发散.
解析 (1)设![]() =c(c>0或+∞),取实数d(0<d<c),则∃N∈N*,当n≥N时有(https://www.xing528.com)
=c(c>0或+∞),取实数d(0<d<c),则∃N∈N*,当n≥N时有(https://www.xing528.com)
因此数列![]() 单调减少,且显然有下界,所以
单调减少,且显然有下界,所以![]() 收敛,记为
收敛,记为![]() =λ.又由于级数
=λ.又由于级数![]() 的部分和Sm满足
的部分和Sm满足
所以级数![]() 收敛,再由(1)式,应用比较判别法得级数
收敛,再由(1)式,应用比较判别法得级数![]() 收敛,因此级数
收敛,因此级数![]() 收敛.
收敛.
(2)设![]() =c(c<0或-∞),取实数d(c<d<0),则∃N∈N*,当n≥N时有
=c(c<0或-∞),取实数d(c<d<0),则∃N∈N*,当n≥N时有
由此可得n≥N时有
由于级数![]() 发散,所以级数
发散,所以级数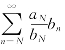 发散,再由(2)式,应用比较判别法得级数
发散,再由(2)式,应用比较判别法得级数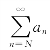 发散,因此级数
发散,因此级数![]() 发散.
发散.
例7.11(精选题) 设函数φ(x)是(-∞,+∞)上连续的周期函数,周期为1,且![]() =0,函数f(x)在[0,1]上有连续的导数,an=
=0,函数f(x)在[0,1]上有连续的导数,an=![]() ,证明:
,证明: 收敛.
收敛.
解析 作积分换元,令nx=t,则
令G(x)=![]() ,则G(0)=0,G′(x)=φ(x),且
,则G(0)=0,G′(x)=φ(x),且
所以G(x)是在(-∞,+∞)上连续可导的周期函数,于是G(x)在(-∞,+∞)上有界,记|G(x)|≤M1.∀x∈(-∞,+∞),有
因f′(x)在[0,1]上连续,所以f′(x)在[0,1]上有界,即∀x∈[0,1]有|f′(x)|≤M2.于是
而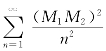 收敛,故由比较判别法得
收敛,故由比较判别法得![]() 收敛.
收敛.
例7.12(浙江省2009年竞赛题) 设fn(x)=![]() +x-r,其中r>0.(1)证明:fn(x)在(0,+∞)内有惟一的零点xn;(2)求r为何值时级数
+x-r,其中r>0.(1)证明:fn(x)在(0,+∞)内有惟一的零点xn;(2)求r为何值时级数![]() 收敛,为何值时级数
收敛,为何值时级数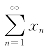 发散.
发散.
解析 (1)因为x>0时,∀n∈N*,有fn(x)连续,且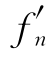 (x)=
(x)=![]() +1>0,所以fn(x)严格增.又因为
+1>0,所以fn(x)严格增.又因为
根据零点定理,fn(x)在(0,r)(⊂(0,+∞))内有惟一的零点xn.
(2)当0<r<1时,![]() ,又由fn(x)严格增可知0<xn<rn,而
,又由fn(x)严格增可知0<xn<rn,而![]() 收敛,由比较判别法可得级数
收敛,由比较判别法可得级数![]() 收敛.
收敛.
当r>1时,因![]() =0,所以只要n充分大,就有
=0,所以只要n充分大,就有
由fn(x)严格增可知xn>![]() >0,而
>0,而![]() 发散,由比较判别法得级数
发散,由比较判别法得级数![]() 发散.
发散.
当r=1时,因为
其中α=![]() ,由于
,由于
故![]() <0.由fn(x)严格增可知xn>
<0.由fn(x)严格增可知xn>![]() >0,由比较判别法得级数
>0,由比较判别法得级数![]() 发散.
发散.
综上所述,当0<r<1时,级数![]() 收敛;当r≥1时,级数
收敛;当r≥1时,级数![]() 发散.
发散.
例7.13(精选题) 设函数f(x)在|x|≤1上有定义,在x=0的某邻域内有连续的二阶导数,x≠0时f(x)≠0,当x→0时f(x)是x的高阶无穷小,且∀n∈N,有
证明:级数![]() 收敛.
收敛.
解析 因x→0时f(x)是x的高阶无穷小,且f(x)在x=0附近有连续的二阶导数,所以f(0)=0,f′(0)=0,且∃K>0,使|x|充分小时|f″(x)|≤K.应用马克劳林展式,有
这里ξ介于0与x之间.当|x|充分小时,|f″(ξ)|≤K,所以n充分大时,有
由于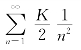 收敛,所以级数
收敛,所以级数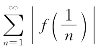 收敛.
收敛.
由于
又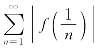 收敛时
收敛时![]() 收敛,因而
收敛,因而![]() 也收敛.应用比较判别法得级数
也收敛.应用比较判别法得级数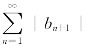 收敛,由此得
收敛,由此得![]() 也收敛.因为
也收敛.因为
应用比较法即得级数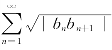 收敛.
收敛.
例7.14(精选题) (1)先讨论级数![]() 的敛散性,又已知xn=1+
的敛散性,又已知xn=1+![]() +…+
+…+![]() -ln(1+n),证明数列{xn}收敛;
-ln(1+n),证明数列{xn}收敛;
(2)求![]()
解析 (1)应用ln(1+x)的马克劳林展式,有
所以当n充分大时,有
而级数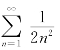 收敛,所以级数
收敛,所以级数![]() 收敛.该级数的部分和为
收敛.该级数的部分和为
所以数列{xn}收敛.
(2)由于![]() =0,设xn→A,则
=0,设xn→A,则
应用洛必达法则,有
所以![]() =1,由(*)式即得
=1,由(*)式即得
例7.15(北京市1992年竞赛题) 设f(x)=![]() ,求证级数
,求证级数![]() 收敛,并求其和.
收敛,并求其和.
解析 令F(x)=(1-x-x2)f(x),则F(x)=1.根据莱布尼兹公式,对上式两边求(n+2)阶导数,有
令x=0得
于是
an+2=an+1+an
且a0=![]() =1,归纳可得n→∞时有an→∞.原级数的部分和
=1,归纳可得n→∞时有an→∞.原级数的部分和
于是级数![]() 收敛,且和为2.
收敛,且和为2.
例7.16(莫斯科工程物理学院1975年竞赛题) 试举出一个收敛的正项级数![]() 其中
其中![]()
解析 当n为某正整数的平方时,取an=![]() ,当n不是某正整数的平方时,取
,当n不是某正整数的平方时,取![]() 即
即![]() 为
为
这里an≠![]() 下面证明该级数是收敛的.由于
下面证明该级数是收敛的.由于
收敛,所以加括号后级数
也收敛.又由于级数
收敛,所以(3)与(4)式逐项相减后所得级数
也收敛.再将收敛级数(5)与(2)逐项相加即得级数(1)收敛.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




