例6.6（江苏省1994年竞赛题） 曲线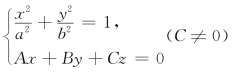
所围平面区域D的面积为________.
解析 因平面Ax+By+Cz=0的法向量的方向余弦为
这里u=
，平面区域D在xy平面上的投影为椭圆
，其面积为πab，所以D的面积为
例6.7（江苏省2000年竞赛题） 过点（2，0，-3）且与直线
垂直的平面方程是（ ）
A.-16（x-2）+14y+11（z+3）=0
B.（x-2）-2y+4（z+3）=0
C.3（x-2）+5（y-0）-2（z+3）=0
D.-16（x+2）+14y+11（z-3）=0
解析 直线的方向向量为
l=（1，-2，4）×（3，5，-2）=-（16，-14，-11）(www.xing528.com)
所以所求平面的法向量为n=（-16，14，11），平面方程为
-16（x-2）+14（y-0）+11（z+3）=0
故选A.
例6.8（江苏省2000年竞赛题） 通过直线
的平面方程是_________________.
解析 直线L1的方向向量为l=（2，3，2），且通过点P1（-1，2，-3），直线L2的方向向量为l=（2，3，2），且通过点P2（3，-1，1）.于是所求平面的法向量为
于是所求平面方程为x-z=2.
例6.9（浙江省2006年竞赛题） 求过点（1，2，3）且与曲面z=x+（y-z）3的所有切平面皆垂直的平面方程.
解析 令F=z-x-（y-z）3=0，则曲面上过一点（x，y，z）的切平面法向量为n=
=（-1，-3（y-z）2，1+3（y-z）2）.记n1=（1，1，1），由于n·n1=-1-3（y-z）2+1+3（y-z）2≡0，所以n1⊥n，因此所求平面方程为（x-1）+（y-2）+（z-3）=0，即x+y+z-6=0.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
