向量运算示例解析-高数竞赛题解析教程

例6.1（江苏省1994年竞赛题）　设a和b是非零常向量，|b|=2，〈a，b〉=则=_________.

例6.2（江苏省1991年竞赛题）　已知a为单位向量，a+3b垂直于7a-5b，a-4b垂直于7a-2b，则向量a与b的夹角为________.

解析　a为单位向量，故|a|=1.因两向量垂直的充要条件是它们的数量积为0，所以

即

由此可解得a·b=|b|2=1，于是

例6.3（江苏省2006年竞赛题）　已知A，B，C，D为空间的4个定点，AB与CD的中点分别为E，F，|EF|=a（a为正常数），P为空间的任一点，则的最小值为________.

解析　如图，在点E，F，P所在平面上建立直角坐标系，并令EF的中点为坐标原点，方向为x轴，则E，F的坐标为E设P的坐标为（x，y），因为又=，所以

由此可得：当x=y=0时，原式取最小值-a2.

例6.4（江苏省1996年竞赛题）　设α与β均为单位向量，其夹角为，则以α+2β与3α+β为邻边的平行四边形的面积为________.

解析　平行四边形的面积(www.xing528.com)

S=|（α+2β）×（3α+β）|=|α×β+6β×α|

=|α×β-6α×β|=|-5α×β|

=5|α×β|=5|α||β|sin〈α，β〉=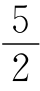

例6.5（江苏省2010年竞赛题）　已知正方体ABCD-A1B1C1D1的边长为2，E为D1C1的中点，F为侧面正方形BCC1B1的中心.

（1）试求过点A1，E，F的平面与底面ABCD所成的二面角的值；

（2）试求过点A1，E，F的平面截正方体所得到的截面的面积.

解析　（1）建立如图所示坐标系，则A1（2，0，2），E（0，1，2），F（1，2，1），=（-1，2，-1），=（1，1，-1），n　==（1，2，3），底面ABCD的法向量为k=（0，0，1），故所求的二面角θ为

（2）设CD的中点为G，则四边形ABCG的面积为S1=3，则所求截面的面积为S=