【摘要】：1）空间曲面的一般方程为F（x，y，z）=0，或写为z=f（x，y）.2）球面：球面方程的一般形式为x2+y2+z2+2ax+2by+2cz+d=0球面的标准方程是（x-a）2+（y-b）2+（z-c）2=R2这里（a，b，c）为球心，R为半径.3）柱面：方程F（x，y）=0表示母线平行于z轴的柱面，准线为方程F（y，z）=0表示母线平行于x轴的柱面，准线为方程F（z，x）=0表示母线平行于y轴的
1）空间曲面的一般方程为F（x，y，z）=0，或写为z=f（x，y）.
2）球面：球面方程的一般形式为
x2+y2+z2+2ax+2by+2cz+d=0
球面的标准方程是
（x-a）2+（y-b）2+（z-c）2=R2
这里（a，b，c）为球心，R为半径.
3）柱面：方程F（x，y）=0表示母线平行于z轴的柱面，准线为
方程F（y，z）=0表示母线平行于x轴的柱面，准线为
方程F（z，x）=0表示母线平行于y轴的柱面，准线为
4）旋转曲面：xy平面上的曲线y=f（x2）绕y轴旋转一周的旋转曲面方程为y=f（x2+z2）；xy平面上的曲线x=g（y2）绕x轴旋转一周的旋转曲面方程为x=g（y2+z2）.其他坐标平面内的曲线绕某坐标轴旋转所得旋转曲面的方程类似可得.
5）二次曲面的标准方程(www.xing528.com)
1；（2）单叶
（3）双叶双曲面
；（4）二次锥面
（6）
6）空间曲面的切平面与法线
已知空间曲面Σ：F（x，y，z）=0，若函数F可微，点P（x0，y0，z0）∈Σ，则
为曲面Σ在点P的法向量；曲面Σ在点P的切平面方程为
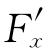（P）（x-x0）+
（P）（y-y0）+
（P）（z-z0）=0
曲面Σ在点P的法线方程为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
