高数竞赛题解析:多元函数积分应用题

例5.68（北京市1988年竞赛题）　求由曲面z=x2+y2和z=2-所围成的体积V和表面积S.

解析　由z=x2+y2，z=2-联立解得z1=1，z2=4（舍去），所围部分在xOy平面上的投影区域D为x2+y2≤1，于是

例5.69（江苏省1991年竞赛题）　有一形状为直角三角形的薄铜片，其质量面密度f（x，y）=k（1-x-2y），x≥0，y≥0，1-x-2y≥0，k为正常数.今从中截取一矩形铜片（该矩形两条邻边位于三角形的两条直角边上）使其质量最大，求该矩形铜片质量与原直角三角形铜片质量之比.

解析　如图，设矩形铜片与原点O相对的顶点为（x0，y0），则1-x0-2y0=0.三角形铜片D的质量为

设矩形铜片为D1，则矩形铜片的质量为

当y0=，x0=时m取最大值所以所求质量之比为

例5.70（江苏省2000年竞赛题）　已知两个球的半径分别是a和b（a＞b），且小球球心在大球球面上，试求小球在大球内的那一部分的体积.

解析　方法1　用二重积分计算.如图，设大球面的方程为

x2+y2+z2=a2

小球面的方程为

x2+y2+（z-a）2=b2

两球面的交线在xy平面上的投影所围的区域D为x2+y2≤，则所求立体的体积为

方法2　用定积分计算.如图，设大圆的方程为x2+y2=a2，小圆的方程为x2+（y-a）2=b2.两圆方程联立解得交点的纵坐标为y0=所求立体为两圆公共区域绕y轴旋转一周的旋转体，其体积为

这里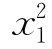=b2-（y-a）2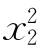，=a2-y2.于是

例5.71（江苏省1991年竞赛题）　求由曲面x2+y2=cz，x2-y2=±a2，xy=±b2和z=0围成区域的体积（其中a，b，c为正实数）.

解析　题中6个曲面关于yz平面对称，关于zx平面也对称，yz平面与zx平面将该区域分为4块等体积区域，将第一卦限的一块投影到xy平面上得区域D.其中区域OABO记为D1，∠AOB=α；区域OBCO记为D2，∠AOC记为β（如图所示）.的极坐标分别为

因此立体区域的体积为

由于ρ1（α）=ρ2（α），ρ2（β）=ρ3（β），所以tan2α=，tan2β=于是

例5.72（莫斯科食品工业学院1977年竞赛题）　将地球看作为半径为R的球体，假设大气层的质量分布密度服从规律p（h）=Re-kh，这里h为质点距离地球表面的高度，k为正常数，试求地球大气层的质量.(www.xing528.com)

解析　以地球中心为坐标原点建立空间直角坐标系，采用球坐标计算，大气层的质量为

例5.73（南京工业大学2009年竞赛题）　试求曲线上的点到间一段的孤长.

解析　设的参数方程为

则

例5.74（江苏省2002年竞赛题）　设曲线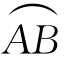的方程为x2+y2=4y-3（x≥0），一质点P在力F的作用下沿曲线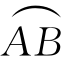从点A（0，1）运动到点B（0，3），力F的大小等于点P到定点M（2，0）的距离，其方向垂直于线段MP，且与y轴正向的夹角为锐角，求力F对质点P所作的功.

解析　根据题意，得=（x-2，y），F=（y，2-x），功

其中D为与y轴所围区域.

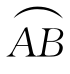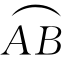例5.75（江苏省2002年竞赛题）　已知曲线的极坐标方程为ρ=1+一质点P在力F的作用下沿曲线从点A（0，-1）运动到点B（0，1），力F的大小等于点P到定点M（3，4）的距离，其方向垂直于线段MP，且与y轴正向的夹角为锐角，求力F对质点P所作的功.

解析　根据题意，得=（x-3，y-4），F=（y-4，3-x），功

其中D为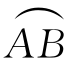与y轴所围区域.

例5.76（莫斯科技术物理学院1976年竞赛题）　在区域＜x2+y2+z2＜4上，函数f（x，y，z）与g（x，y，z）具有二阶连续的偏导数，Σ为球面x2+y2+z2=1的外侧，求单位时间内向量gradf×gradg通过Σ的流量.

记P=应用高斯公式，有

例5.77（陕西省1999年竞赛题）　给定面密度为1的平面薄板D：x2≤y≤1，求该薄板关于过D的重心和点（1，1）的直线的转动惯量.

解析　令重心的坐标为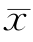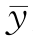（，），由于D关于x=0对称，可知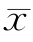=0，且

于是D的重心为

过重心与点（1，1）的直线L的方程为2x-5y+3=0.由于D上任一点（x，y）到直线L的距离为d=，故所求转动惯量为

应用奇偶函数的积分性质可知

因此，所求转动惯量为