高斯公式解题例题及解析

例5.61（南京大学1993年竞赛题）　设Г为yOz平面上的一条闭曲线，S是以Г为边界的有向光滑曲面的前侧，求

解析　记

P=x（z2-y2），Q=y（x2-z2），R=z（y2-x2）

则=0，故曲面积分与曲面无关.记闭曲线Г所围的平面区域为D，取前侧，则

例5.62（江苏省2008年竞赛题）　设Σ为x2+y2+z2=1（z≥0）的外侧，求

解析　记Σ1：x2+y2≤1，z=0，取下侧，P=xz2，Q=yz2，R=2z（x2+y2），应用高斯公式，则

例5.63（全国大学生2011年决赛题）　已知S是空间曲线绕y轴旋转生成的椭球面的上半部分（z≥0），取上侧，Π是S在P（x，y，z）点处的切平面，ρ（x，y，z）是原点到切平面Π的距离，λ，μ，ν表示S的正法向的方向余弦，计算：

（1）

（2）

解析　根据题意，可得旋转曲面S的方程为x2+3y2+z2=1（z≥0）.设曲面S上任一点P（x，y，z）点处的切平面Π的方程为xX+3yY+zZ=1，于是

记，则曲面S的外法向量的方向余弦为

（1）令Σ：z=0（x2+3y2≤1），取下侧.记S与Σ包围的区域为Ω，则

（2）记号同上，计算过程同上，有

例5.64（江苏省1996年竞赛题）　计算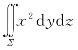+y2dzdx+z2dxdy，其中Σ为柱面x2+y2=1界于z=0与x+y+z=2之间部分的外侧.

解析　记Σ1：x+y+z=2（界于x2+y2≤1内的部分），取上侧；记Σ2：z=0（界于x2+y2≤1内的部分），取下侧.记Σ，Σ1，Σ2所包围的立体区域为Ω.在Ω上应用高斯公式，记D：x2+y2≤1，则

又

于是(www.xing528.com)

例5.65（江苏省2008年竞赛题）　设Σ为x2+y2+z2=1（z≥0）的外侧，连续函数f（x，y）满足

求f（x，y）.

解析　设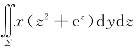+y（z2+ez）dzdx+［zf（x，y）-2ez］dxdy=a，则f（x，y）=2（x-y）2+a.设D为xy平面上的圆x2+y2≤1，Σ1为D的下侧，Ω为Σ与Σ1包围的区域，应用高斯公式，有

故a=于是f（x，y）=2（x-y）2+

例5.66（江苏省2010年竞赛题）　应用高斯公式计算

其中Σ：x2+y2+z2=2z.

解析　令F=x2+y2+z2-2z=0，则Σ的外侧的法向量为n==（2x，2y，2z-2），其方向余弦为n°=（cosα，cosβ，cosγ）=（x，y，z-1），则

例5.67（南京大学1995年竞赛题）　设φ（x，y，z）为原点到椭球面Σ：

上点（x，y，z）处的切平面的距离，求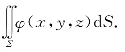

解析　方法1　椭球面=1任一点P（x，y，z）处的切平面方程为=1，坐标原点到切平面的距离

记u=，则φ（x，y，z）=于是

因椭球面Σ上P点处的外侧法向量的方向余弦为

由此化简（1）式得

方法2　φ（x，y，z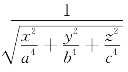）=的求法同方法1，因φ（x，y，z）分别关于x，y，z皆为偶函数，Σ关于x=0对称，关于y=0对称，关于z=0对称，设Σ位于第一卦限的那部分曲面为Σ1，则

曲面Σ1的方程为z=（x≥0，y≥0），Σ1在xy平面上的投影为D1=由于

代入（2）式，并令x=ρacosθ，y=ρbsinθ，则