例5.45(江苏省1998年竞赛题) 若φ(y)的导数连续,φ(0)=0,曲线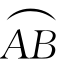 的极坐标方程为ρ=a(1-cosθ),其中a>0,0≤θ≤π,A与B分别对应于θ=0与θ=π,求
的极坐标方程为ρ=a(1-cosθ),其中a>0,0≤θ≤π,A与B分别对应于θ=0与θ=π,求![]() [φ(y)ex-πy]dx+[φ′(y)ex-π]dy.
[φ(y)ex-πy]dx+[φ′(y)ex-π]dy.
解析 设曲线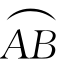 与线段
与线段![]() 所围区域为D(如上图所示),又设
所围区域为D(如上图所示),又设
P=φ(y)ex-πy,Q=φ′(y)ex-π
应用格林公式,有
由于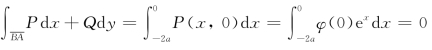 ,于是
,于是
例5.46(全国大学生2012年决赛题) 设连续可微函数z=z(x,y)由方程F(xz-y,x-yz)=0(其中F(u,v)有连续的偏导数)惟一确定,L为正向单位圆周,试求
解析 记f(x,y,z)=F(xz-y,x-yz),应用隐函数方程求偏导数公式有
记P=-(2xz+yz2),Q=xz2+2yz,单位圆包围的区域记为D,应用格林公式有
例5.47(江苏省2006年竞赛题) 已知Г是y=asinx(a>0)上从(0,0)到(π,0)的一段曲线,a=_______________时,曲线积分∫Г(x2+y)dx+(2xy +![]() )dy取最大值.
)dy取最大值.
解析 设Г与![]() 所围区域为D(如图所示),在D上应用格林公式,记P=x2+y,Q=2xy+
所围区域为D(如图所示),在D上应用格林公式,记P=x2+y,Q=2xy+![]() ,则
,则
令![]() =2-aπ=0得惟一驻点a=
=2-aπ=0得惟一驻点a=![]() ,由于
,由于![]() ,所以
,所以![]() 为极大值,即最大值,故a=
为极大值,即最大值,故a=![]()
例5.48(江苏省2008年竞赛题) 设Γ为x2+y2=2x(y≥0)上从O(0,0)到A(2,0)的一段弧,连续函数f(x)满足
f(x)=x2+∫Γy[f(x)+ex]dx+(ex-xy2)dy
求f(x).
解析 设∫Γy[f(x)+ex]dx+(ex-xy2)dy=a,则f(x)=x2+a,记Γ与![]() 包围的区域为D,应用格林公式,有
包围的区域为D,应用格林公式,有
解得a=![]() 于是f(x)=x2+
于是f(x)=x2+![]()
例5.49(北京市1996年竞赛题) 设函数f(x,y)在区域D:x2+y2≤1上有二阶连续偏导数,且![]() ,证明
,证明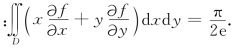
解析 运用极坐标变换,有
其中![]() 可看作沿半径为ρ(0≤ρ≤1)的圆周L的逆向的曲线积分.因x=ρcosθ,y=ρsinθ,所以dx=-ρsinθdθ,dy=ρcosθdθ.记D是半径为ρ的圆域,应用格林公式,上述积分化为
可看作沿半径为ρ(0≤ρ≤1)的圆周L的逆向的曲线积分.因x=ρcosθ,y=ρsinθ,所以dx=-ρsinθdθ,dy=ρcosθdθ.记D是半径为ρ的圆域,应用格林公式,上述积分化为
例5.50(精选题) 求曲线积分∫Γ|y-x|dy+zdz,其中Γ为
其方向与z轴正方满足右手法则.
解析 曲线Γ的方程可写为
将Γ的位于y=x上方的部分记为Γ1,位于y=x下方的部分记为Γ2,Γ与y=x的交点记为A,B(如图).将Γ所围的圆域用![]() 分为D1与D1,则
分为D1与D1,则
例5.51(江苏省1996年竞赛题) 计算曲线积分![]()
(1)C是正向圆周(x-a)2+(y-a)2=a2;
(2)C是正向曲线|x|+|y|=1.
解析 记P=![]() ,则
,则
(1)设D1:(x-a)2+(y-a)2≤a2,P,Q在D1内偏导数连续,应用格林公式,有
(2)设D2:|x|+|y|≤1,P和Q在D2内偏导数不连续,故不能应用格林公式.在C内作圆Г:x2+y2=![]() ,取负向.
,取负向.
设C与Г包围的区域为D3(如图所示),在区域D3上应用格林公式,有
由Γ的参数方程x=εcosθ,y=εsinθ,得(https://www.xing528.com)
例5.52(精选题) 已知P(x,y)=![]() (1)求常数a和λ,使得∫LPdx+Qdy在区域D={(x,y)|x2+y2>0}上与路径无关;(2)求Pdx+Qdy在D中的原函数.
(1)求常数a和λ,使得∫LPdx+Qdy在区域D={(x,y)|x2+y2>0}上与路径无关;(2)求Pdx+Qdy在D中的原函数.
解析 (1)在区域D上,P,Q∈C(1),由于曲线积分与路径无关的充要条件是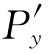 =
=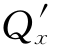 ,而
,而
所以λ-1=1,4λ=2a,即λ=2,a=4,此时
(2)令Pdx+Qdy=du,则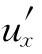 =P,
=P,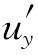 =Q,于是
=Q,于是
代入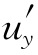 =Q得
=Q得
即φ′(y)=0.取φ(y)=C,得所求的原函数为u=![]() +C.
+C.
例5.53(江苏省2004年竞赛题) 设f(x)连续可导,f(1)=1,G为不包含原点的单连通域,任取M,N∈G,在G内曲线积分![]() 与路径无关.
与路径无关.
(1)求f(x);
(2)求![]() ,其中Г为
,其中Г为![]() ,取正向.
,取正向.
解析 记P(x,y)=![]() ,因为在G内曲线积分
,因为在G内曲线积分![]() 与路径无关,所以∀(x,y)∈G,有
与路径无关,所以∀(x,y)∈G,有![]() 即
即
由此推得yf′(y)=2f(y),又f(1)=1,解此变量可分离的微分方程得f(y)=y2.于是f(x)=x2.
取小椭圆Гε:2x2+y2=ε2,取正向,ε为充分小的正数,使得Гε位于Г的内部.设Г与Гε所包围的区域为D.在D上,P和Q的一阶偏导数连续,且![]() ,应用格林公式得
,应用格林公式得
这里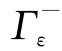 为负向(即顺时针方向),于是
为负向(即顺时针方向),于是
例5.54(莫斯科钢铁与合金学院1976年竞赛题) 计算曲线积分
其中u=ax+by,v=cx+dy(ad-bc≠0),L为xy平面上环绕坐标原点的单闭曲线,取逆时针方向.
解析 将u=ax+by,v=cx+dy代入原式得
记P=![]() ,则
,则
由于(u,v)=(0,0)⇔(x,y)=(0,0),所以在(x,y)≠(0,0)的区域上,曲线积分与路线无关.在单闭曲线L内部取椭圆Г:(ax+by)2+(cx+dy)2=ρ2(逆时针方向),ρ>0充分小,则
这里D为椭圆Г包围的区域.对上式右边的二重积分作换元变换,令u=ax+by,v=cx+dy,则
于是
这里±的选取是当ad-bc>0时取正号,当ad-bc<0时取负号.
例5.55(莫斯科电气学院1976年竞赛题) 设P(x,y),Q(x,y)在全平面上具有连续的一阶偏导数,沿着平面上的任意半圆周L:y=y0+![]() 曲线积分∫LP(x,y)dx+Q(x,y)dy=0,其中x0,y0为任意实数,R为任意正实数,求证:(1)P(x,y)≡0;(2)
曲线积分∫LP(x,y)dx+Q(x,y)dy=0,其中x0,y0为任意实数,R为任意正实数,求证:(1)P(x,y)≡0;(2)![]() ≡0.
≡0.
解析 (1)∀(x0,y0)∈R2,∀R>0,以(x0,y0)为圆心,以R为半径作上半圆周L,取逆时针方向,起点为A(x0-R,y0),终点为B(x0+R,y0),则
对(1)式右端应用积分中值定理,∃(ξ,η)∈D,有
对(1)式左端有
对此式右端应用定积分中值定理,∃c∈(x0-R,x0+R),有
将(2)式与(3)式代入(1)式得
令R→0,此时c→x0,(ξ,η)→(x0,y0),得P(x0,y0)=0,由(x0,y0)∈R2的任意性,即得P(x,y)≡0.
(2)(反证法)假设∃(a,b)∈R2,使得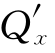 (a,b)>0(或<0).由于Q∈C(1)(R2),所以∃(a,b)的邻域U,使得
(a,b)>0(或<0).由于Q∈C(1)(R2),所以∃(a,b)的邻域U,使得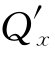 |(x,y)∈U>0(或<0),在邻域U内取上半圆周L,则
|(x,y)∈U>0(或<0),在邻域U内取上半圆周L,则
此为矛盾式,故有![]() ≡0.
≡0.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




