高等数学竞赛题解析教程：曲线积分计算实例

例5.39（江苏省2000年竞赛题）　计算曲线积分

其中L为曲线y2=-（x-3）上点A（-2，-1）沿逆时针方向到该曲线上点B（3，0）的一段曲线.

解析　令P=x4+4xy3，Q=6x2y2-5y4，则

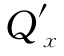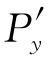==12xy2

且P，Q在全平面上偏导数连续，所以Pdx+Qdy存在原函数.通过观察法可以看出u=+2x2y3-y5，使得du=Pdx+Qdy.于是

例5.40（南京大学1996年竞赛题）　求，其中曲线C由方程组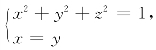给定.

解析　曲线C的参数方程为x=z=sinθ（0≤θ≤2π），于是

例5.41（南京工业大学2009年竞赛题）　设Γ是由点（1，0）经y=1-x2到（-1，0）曲线段，则=________.

解析　令P（x，y）=则

所以在不包含（0，0）的单连通区域内，与路径无关.作圆x2+y2=1（y≥0），从（1，0）到（-1，0）的上半圆周记为L，则L：x=cosθ，y=sinθ，θ从0到π，故

例5.42（江苏省2012年竞赛题）　已知Γ为x2+y2+z2=6y与x2+y2=4y（z≥0）的交线，从z轴正向看上去为逆时针方向，计算曲线积分

解析　方法1　记曲线Γ的x≥0的部分与x≤0的部分分别为Γ1与Γ2，其参数方程分别为

分别在Γ1和Γ2上积分，有

两式相加，则

方法2　记P=x2+y2-z2，Q=y2+z2-x2，R=z2+x2-y2，Σ为球面x2+y2+z2=6y位于交线Γ上方的部分，取上侧.利用斯托克斯公式，则

采用统一投影法计算.设D=｛（x，y）|x2+y2≤4y｝，因(www.xing528.com)

故

即

例5.43（浙江省2009年竞赛题）　设R（x，y，z）=f（z-t）dt，其中f的导函数连续，曲面S为z=x2+y2被y+z=1所截的下面部分，取内侧，L为S的正向边界，求

解析　因为在L上z=x2+y2，所以

记R（z）=，代入原式化简，有

这里A为曲线L上任一点.记P=0，Q=x3，R=R（z），应用斯托克斯公式，则

曲面S在O-xy平面上的投影为D关于x=0对称，于是

例5.44（全国大学生2009年初赛题）　设平面区域D=｛（x，y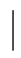）0≤x≤π，0≤y≤π｝，L为D的正向边界，试证：

（1）∮Lxesinydy-ye-sinxdx=∮Lxe-sinydy-yesinxdx；

（2）∮Lxesinydy-ye-sinxdx≥

解析　（1）设正方形曲线L的4个顶点按逆时针排分别为O，A，B，C，则

两式右端相等，所以（1）得证.

（2）由于ex=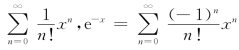，所以

由（1）问以及积分的保号性得