【摘要】：例5.27（南京大学1996年竞赛题）设f（x）连续，f（0）=k，Vt由0≤z≤k，x2+y2≤t2确定，试求，其中F（t）=解析记D：x2+y2≤t2，则故例5.28（江苏省2006年竞赛题）曲线绕z轴旋转一周生成的曲面与z=1，z=2所围成的立体区域记为Ω.（1）求（x2+y2+z2）dxdydz；（2）求解析曲面方程为x2+y2=2z，记D（z）：x2+y2≤（1）方法1方法2例5
例5.27（南京大学1996年竞赛题） 设f（x）连续，f（0）=k，Vt由0≤z≤k，x2+y2≤t2确定，试求
，其中F（t）=
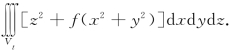
解析 记D：x2+y2≤t2，则
故
例5.28（江苏省2006年竞赛题） 曲线
绕z轴旋转一周生成的曲面与z=1，z=2所围成的立体区域记为Ω.
（1）求
（x2+y2+z2）dxdydz；
（2）求
解析 曲面方程为x2+y2=2z，记D（z）：x2+y2≤
（1）方法1
方法2
例5.29（南京大学1993年竞赛题） 求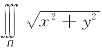
dxdydz，其中Ω为由曲面z=
所围成的立体.
解析 方法1（用球坐标变换） 令
x=rsinφcosθ，y=rsinφsinθ，z=rcosφ(https://www.xing528.com)
则0≤r≤1，0≤φ≤
，0≤θ≤2π，故
方法2（用柱坐标变换） 令
x=ρcosθ，y=ρsinθ，z=z
则ρ≤z≤
，0≤ρ≤
，0≤θ≤2π，故
例5.30（北京市1997年竞赛题） 设f（x）在区间［0，1］上连续，且
=m，试求
解析 令F（u）=
，则F（0）=0，F（1）=m，F′（u）=f（u）.由于
于是
例5.31（江苏省2002年竞赛题） 设f（u）在u=0可导，f（0）=0，Ω：x2+y2+z2≤2tz，求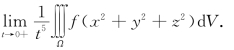
解析 先用球坐标计算三重积分，有
于是
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
