2016高等数学竞赛题解析：曲线积分基本概念与计算

1）空间曲线的弧长

设曲线Γ的参数方程为

x=φ（t），y=ψ（t），z=ω（t）

其中t∈［α，β］，曲线Γ上的点与［α，β］上的点一一对应，函数φ，ψ，ω连续可导，则曲线Γ的弧长为

2）第一型曲线积分的定义与性质

设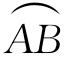是可求长的连续曲线，函数f（x，y，z）在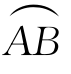上定义，将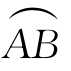任意分割为n个小弧段Γi（i=1，2，…，n），Γi的弧长记为Δli，Γi的直径为di，λ=在Γi上任取点（xi，yi，zi），则函数f沿曲线的第一型曲线积分定义为

这里右端的极限存在，且与分割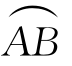的方式无关，与点（xi，yi，zi）的取法无关.

当f在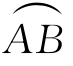上连续时，f在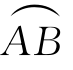上的第一型曲线积分存在，即可积.

定理（奇偶函数在对称曲线上的积分）

（1）若曲线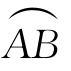上的点关于x=0对称，f在上可积，则

这里Γ1是曲线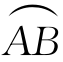的x≥0的部分曲线.

（2）若曲线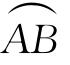上的点关于y=0对称，f在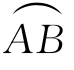上可积，则

这里Γ2是曲线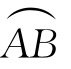的y≥0的部分曲线.

（3）若曲线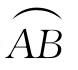上的点关于z=0对称，f在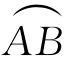上可积，则

3）第一型曲线积分的计算

设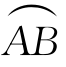为空间的连续曲线，其参数方程为(www.xing528.com)

x=φ（t），y=ψ（t），z=ω（t）

其中t∈［α，β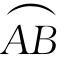］，上的点与［α，β］上的点一一对应，函数φ，ψ，ω连续可导，函数f（x，y，z）在上连续，则

4）第二型曲线积分的定义

设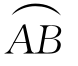为空间的光滑曲线，的顺向的单位切向量为（cosα，cosβ，cosγ），函数P（x，y，z），Q（x，y，z），R（x，y，z）在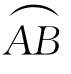上定义，将任意地分割为n个小弧段Γi（i=1，2，…，n），Γi的弧长记为Δli，Γi的直径为di，令λ=，在Γi上任取点Mi（xi，yi，zi），记

Δxi=Δli·cosαi，Δyi=Δli·cosβi，Δzi=Δli·cosγi

则函数P，Q，R沿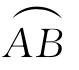从A到B的第二型曲线积分定义为

式中三个极限皆存在，且与分割的方式无关，与点（xi，yi，zi）的取法无关.

当函数P，Q，R皆在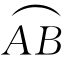上连续时，对应的第二型曲线积分存在，即可积.

5）第二型曲线积分的计算

设曲线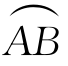的方程为

x=φ（t），y=ψ（t），z=ω（t）

其中t∈［α，β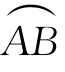］，的点与［α，β］的点一一对应，函数φ，ψ，ω在［α，β］上连续可导，函数P，Q，R在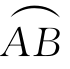上连续，则

其中，第一式为t增大时，对应的点在曲线上从A到B；第二式为t增大时，对应的点在曲线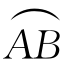上从B到A.

第二型曲线积分在物理上表示一质点在力F=（P，Q，R）作用下，沿曲线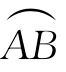从A到B所作的功.