高等数学竞赛题解析教程：求条件极值问题解析

例4.36（江苏省2002年竞赛题）　函数f（x，y）=2x-y+1满足方程x2+y2=5的条件极大值为_________，条件极小值为________.

解析　应用拉格朗日乘数法，令

F=2x-y+1+λ（x2+y2-5）

由方程组

解得驻点为（-2，1），（2，-1），对应的函数值为-4，6，所以条件极大值为6，条件极小值为-4.

例4.37（江苏省1994年竞赛题）　椭球面x2+2y2+4z2=1与平面x+y+z-=0之间的最短距离为_________.

解析　设椭球面上的点P（x，y，z）到平面的距离为d，则

应用拉格朗日乘数法，令

由方程组

解得驻点这两点到平面的距离d分别是故最小距离为

例4.38（江苏省1994年竞赛题）　已知a，b满足求曲线y=x2+ax与直线y=bx所围区域的面积的最大值与最小值.

解析　因为(www.xing528.com)

故a2+b2=1.曲线y=x2+ax与直线y=bx所围图形的面积为

应用拉格朗日乘数法，令

由方程组

解得驻点此时S=又a=0时b=1，此时S=；a=-1时b=0，此时S=所以所求面积的最大值为最小值为

例4.39（江苏省2008年竞赛题）　已知曲面4x2+4y2-z2=1与平面x+y-z=0的交线在xy平面上的投影为一椭圆，求此椭圆的面积.

解析　方法1　椭圆的方程为3x2+3y2-2xy=1.椭圆的中心在原点，在椭圆上任取一点（x，y），它到原点的距离

令F=x2+y2+λ（3x2+3y2-2xy-1），则

由上（1）和（2）两式推得y=x或y=-x，故驻点为

因此d（P1）=d（P2）=，d（P3）=d（P4）=分别为椭圆的长、短轴，于是椭圆的面积为

方法2　椭圆的方程为3x2+3y2-2xy=1.椭圆的中心在原点，作坐标系的旋转变换，令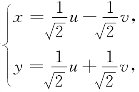代入椭圆方程得2u2+4v2=1，因此a=分别为椭圆的长、短轴，于是椭圆的面积为