高阶偏导数求解技巧解析

例4.21（全国大学生2010年初赛题）　已知函数f（x）有二阶连续导数，设r

解析　应用复合函数求偏导数法则得

应用对称性得

于是

例4.22（浙江省2009年竞赛题）　设g二阶可导，f具有二阶连续偏导数，z=g（xf（x+y，2y）），求=_________.

解析　应用多元复合函数的链锁法则，有

即

例4.23（北京市1990年竞赛题）　设函数u=满足

试求函数f的表达式.

解析　令t=ln（x2+y2），则

同理可得代入原方程得

即得f″（t）==e5t，积分两次得

例4.24（江苏省1998年竞赛题）　已知函数f（x，y）的二阶偏导数皆连续，且

试求（x，2x）与（x，2x）.

解析　在等式f（x，2x）=x2两边对x求全导数得

（x，2x）+2（x，2x）=2x

两边再对x求全导数得

由条件得

在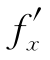（x，2x）=x两边对x求全导数得

将上两式联立解得

例4.25（江苏省2008年竞赛题）　已知函数u（x，y）具有连续的二阶偏导数，算子A定义为A（u）=求A（u-A（u））；（2）利用结论（1），以ξ=，η=x-y为新的自变量，改变方程的形式.

（2）由=0⇔A（u-A（u））=0，又

于是原方程化为=0.

例4.26（精选题）　设函数u=u（x，y）有连续的二阶偏导数，且满足方程

（1）用变量代换ξ=x-y，η=x+y将上述方程化为以ξ，η为自变量的方程；

（2）已知u（x，2x）=x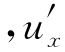（x，2x）=x2，求u（x，y）.

解析　（1）div（gradu）=，于是原方程化为

由于

将（2）式与（3）式代入（1）式得=0.

（2）将方程=0两边对η积分得

此式两边对ξ积分得

u=∫φ（ξ）dξ+g（η）=f（ξ）+g（η）

这里f，g为任意可微函数.于是

u（x，y）=f（x-y）+g（x+y）　（4）(www.xing528.com)

由条件u（x，2x）=x得

f（-x）+g（3x）=x　（5）

（4）式两边对x求偏，导得

=f′（x-y）+g′（x+y）

由条件（x，2x）=x2得

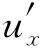（x，2x）=f′（-x）+g′（3x）=x2　（6）

（6）式两边对x积分得

-3f（-x）+g（3x）=x3+C　（7）

联立（5）式与（7）式解得

由此可得

于是由（4）式可得所求函数为

例4.27（北京市2002年竞赛题）　设函数z=f（x，y）具有二阶连续偏导数，且≠0，证明：对任意常数C，f（x，y）=C为一直线的充要条件是

解析　先证必要性.若f（x，y）=C为一直线，则均为常数，故==0，从而等式成立.

再证充分性.设由f（x，y）=C确定隐函数y=y（x），于是f（x，y（x））≡0.两边对x求导得两边再对x求导得

因为代入上式得

由条件得

积分得y=C1x+C2（C1，C2为常数），从而f（x，y）=0为一直线.

例4.28（全国大学生2011年初赛题）　设z=z（x，y）是由方程

确定的隐函数，且具有连续的二阶偏导数，求证：

解析　记f（x，y，z）=，应用隐函数求偏导数法则有

于是

此式两端分别对x，y求偏导数得

（1）式乘x加上（2）式乘y得

例4.29（南京大学1995年竞赛题）　若

解析　因u=1+，所以

由于

所以

例4.30（清华大学1985年竞赛题）　求

对x的n阶导数.

解析　令fk（x）=，则

应用莱布尼兹公式^[1]得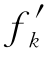（x）==fk-1（x），于是

由于，所以