求多元复合函数与隐函数的偏导数

例4.9（江苏省2004年竞赛题）　设f（x，y）可微，f（1，2）=2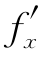，（1，2）=3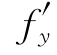，（1，2）=4，φ（x）=f（x，f（x，2x）），则φ′（1）=___________.

解析　应用多元复合函数的链锁法则，有

因f（1，f（1，2））=f（1，2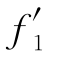）（1，2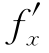）=（1，2）=3，（1，2）=（1，2）=4，故

例4.10（江苏省1998年竞赛题）　设变量x，y，t满足y=f（x，t）及F（x，y，t）=0，且函数f，F的一阶偏导数连续，则=___________________.

解析　由方程组y=f（x，t），F（x，y，t）=0确定y，t是x的一元函数，即有y（x），t（x）.方程两边对x求导得

两式联立消得

例4.11（江苏省2012年竞赛题）　已知函数φ（x），ψ（x），f（x，y）皆可微，设z=f（φ（x+y），ψ（xy）），则=_________.

解析　应用多元复合函数的链锁法则，有

所以

例4.12（江苏省2000年竞赛题）　设z=z（x，y）由方程=0确定（F为任意可微函数），则=________.

解析　应用隐函数求偏导数法则，令f（x，y，z）=，则

于是

例4.13（江苏省2006年竞赛题）　已知由x=zey+z可确定z=z（x，y），则dz（e，0）=_________________.

解析　x=e，y=0时，由e=zez，故z（e，0）=1.令F=zey+z-x，则由隐函数求偏导数公式得

令x=e，y=0，z=1代入得于是

例4.14（南京大学1996年竞赛题）　设y=f（x，t），而t是由方程G（x，y，t）=0所确定的x，y的函数，其中f，G可微，求

解析　令F（x，y，t）=f（x，t）-y=0，则由

确定y=y（x），t=t（x）.方程式（＊）两边对x求导得

由此可解得

例4.15（江苏省2000年竞赛题）　假设u=u（x，y）由方程u=f（x，y，z，t），g（y，z，t）=0和h（z，t）=0确定（f，g，h均为可微函数），求

解析　首先由确定z=z（y），t=t（y）.方程组对y求导数得

由此解得

应用复合函数求偏导数法则得

例4.16（江苏省1994年竞赛题）　设z是由方程组确定的隐函数，则=_________.

解析　在方程组中将x，y视为自变量，将z，t视为隐函数，方程组两边对x求偏导，有

（1）式乘以sinz减去（2）式乘以cosz得(www.xing528.com)

例4.17（江苏省2012年竞赛题）　设函数f（x，y）在平面区域D上可微，线段PQ位于D内，已知点P，Q的坐标分别为P（a，b），Q（x，y），求证：在线段PQ上存在点M（ξ，η），使得

f（x，y）=f（a，b）+（ξ，η）（x-a）+（ξ，η）（y-b）

解析　令F（t）=f（a+t（x-a），b+t（y-b）），则F（t）在［0，1］上连续，在（0，1）内可导，应用拉格朗日中值定理，必∃θ∈（0，1），使得

F（1）-F（0）=F′（θ）（1-0）=F′（θ）　（＊）

因为

F′（t）=（a+t（x-a），b+t（y-b））（x-a）

+（a+t（x-a），b+t（y-b））（y-b）

令ξ=a+θ（x-a），η=b+θ（y-b），点M（ξ，η）显然位于线段PQ上，则

F′（θ）=（ξ，η）（x-a）+（ξ，η）（y-b）

又F（0）=f（a，b），F（1）=f（x，y），代入（＊）式得

f（x，y）=f（a，b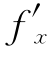）+（ξ，η）（x-a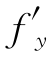）+（ξ，η）（y-b）

例4.18（北京市2000年竞赛题）　设u=f（x，y，z），f是可微函数，若，证明：u仅为r的函数，已知r=

解析　令x=rcosθ·sinφ，y=rsinθ·sinφ，z=rcosφ，则有

u=f（rcosθ·sinφ，rsinθ·sinφ，rcosφ）

则

由得

代入，从而得证u仅为r的函数.

例4.19（浙江省2002年竞赛题）　设二元函数f（x，y）有一阶连续的偏导数，且f（0，1）=f（1，0），证明：单位圆周上至少存在两点满足方程

解析　令g（t）=f（cost，sint），则g（t）一阶连续可导，且g（0）=f（1，0），=f（0，1），g（2π）=f（1，0），所以g（0）==g（2π）.分别在区间上应用罗尔定理，存在，使得

g′（ξ1）=0，g′（ξ2）=0

记（x1，y1）=（cosξ1，sinξ1），（x2，y2）=（cosξ2，sinξ2），由于

所以

即

例4.20（北京市1995年竞赛题）　已知函数z=z（x，y）满足=z2，设u=x，v=，对函数ψ=ψ（u，v），求证=0.

解析　由u=x，v=，有x=u，y=于是