【摘要】:1)偏导数的定义这两式右端的极限存在,称f在(a,b)处可偏导.这两式右端的极限存在,称f在(0,0)处可偏导.2)f(x,y)在(a,b)处可偏导时,f(x,y)在(a,b)处不一定连续.3)偏导数的几何意义当f在(a,b)处对x可偏导时,(a,b)表示曲线在(a,b)的切线对x轴的斜率;当f在(a,b)处对y可偏导时,(a,b)表示曲线在(a,b)的切线对y轴的斜率.4)全微分的定义:若f(x
1)偏导数的定义
这两式右端的极限存在,称f在(a,b)处可偏导.
这两式右端的极限存在,称f在(0,0)处可偏导.
2)f(x,y)在(a,b)处可偏导时,f(x,y)在(a,b)处不一定连续.
3)偏导数的几何意义
当f在(a,b)处对x可偏导时,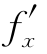 (a,b)表示曲线
(a,b)表示曲线![]() 在(a,b)的切线对x轴的斜率;
在(a,b)的切线对x轴的斜率;
当f在(a,b)处对y可偏导时, (a,b)表示曲线
(a,b)表示曲线![]() 在(a,b)的切线对y轴的斜率.
在(a,b)的切线对y轴的斜率.
4)全微分的定义:若f(x,y)在(a,b)的全增量Δf(x,y)可写为
Δf(x,y)=f(a+Δx,b+Δy)-f(a,b)=AΔx+BΔy+o(ρ) (1)(https://www.xing528.com)
这里ρ=![]() ,则称f(x,y)在(a,b)处可微.
,则称f(x,y)在(a,b)处可微.
当f(x,y)在(a,b)处可微时,f(x,y)在(a,b)处必可偏导,且(1)式中A=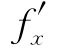 (a,b),B=
(a,b),B=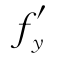 (a,b).
(a,b).
当f(x,y)在(a,b)处可微时,f(x,y)在(a,b)处必连续.
当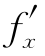 (x,y),
(x,y),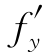 (x,y)在(a,b)处连续时,f(x,y)在(a,b)处必可微(此时称f在(a,b)处连续可微).
(x,y)在(a,b)处连续时,f(x,y)在(a,b)处必可微(此时称f在(a,b)处连续可微).
当f(x,y)在(a,b)处可微时,称
为f(x,y)在(a,b)处的全微分;当f(x,y)在(x,y)处可微时,称
为f(x,y)的全微分.
由于多元初等函数的偏导数仍是多元初等函数,所以多元初等函数在其可偏导处必偏导数连续,因而必可微,其全微分公式(2)与(3)可直接使用.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




