高等数学竞赛题解析：变限定积分的应用

例3.33（江苏省2006年竞赛题）　=________.

解析　应用洛必达法则，则

例3.34（江苏省1996年竞赛题）　若a＞0时，有

则a=________.

解析　上式左端应用洛必达法则求极限，有

原式右端应用洛必达法则求极限，有

所以，故a=36.

例3.35（江苏省2000年竞赛题）　当x→0时，F（x）=f′（t）dt的导数与x2为等价无穷小，求f′（0）.

解析　因为

所以

因为F′（x）与x2为等价无穷小，所以2（f（x）-f（0））与x为等价无穷小，即

所以f′（0）=

例3.36（江苏省2000年竞赛题）　设f′（x）连续，f（0）=0，f′（0）≠0，求

解析　应用洛必达法则与变上限积分求导公式，则

例3.37（上海市1991年竞赛题）　设函数f（x）=x-［x］，其中［x］表示不超过x的最大整数，求极限

解析　根据题意可知f（x）是周期为1的周期函数，且f（x）≥0，当0≤x＜1时有f（x）=x.设n≤x＜n+1，则x→+∞时n→∞，且

应用夹逼准则，原式=

例3.38（江苏省2006年竞赛题）　

解析　令tx=u将定积分换元，再应用洛必达法则，则

例3.39（南京大学1995年竞赛题）　求

解析　应用积分的保向性，有

因为

应用夹逼准则得

例3.40（江苏省2000年竞赛题）　设

求F（x）=

解析　先用变量代换化简定积分，即令x-t=u，则

例3.41（江苏省1998年竞赛题）　已知g（x）是以T为周期的连续函数，且g（0）=1，，求f′（T）.

解析　因为

所以

因g（t）以T为周期，故，g（2T）=g（0）=1，得f′（T）=2T.

例3.42（浙江省2002年竞赛题）　设f（x）连续，且当x＞-1时有

求f（x）.

解析　令y（x）=，则y（0）=1，且y′（x）=f（x），于是有

两边积分得

由y（0）=1可得C=0，所以y（x）=，即

于是

例3.43（江苏省2008年竞赛题）　已知函数f（x）在［a，b］上连续（a＞0），且=0，求证：存在ξ∈（a，b），使得=ξf（ξ）.

解析　令F（x）=，由于f（x）在［a，b］上连续，故F（x）在［a，b］上可导，且F（a）=0，F（b）=0.应用罗尔定理，∃ξ∈（a，b），使得F′（ξ）=0，而F′（x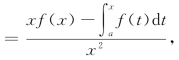）故

例3.44（江苏省2006年竞赛题）　设f（x）在区间［0，+∞）上是导数连续的函数，f（0）=0，|f（x）-f′（x）|≤1，求证：|f（x）|≤ex-1，x∈［0，+∞）.

解析　方法1　∀x＞0，因为

［e-xf（x）］′=e-x（f′（x）-f（x））

两边从0到x积分得

即|f（x）|≤ex-1.

方法2　令F（x）=e-x（f（x）+1），则(www.xing528.com)

F′（x）=e-x（f′（x）-f（x）-1）

由于|f（x）-f′（x）|≤1，所以f′（x）-f（x）-1≤0，于是F′（x）≤0，即F（x）在区间［0，+∞）上单调减，因此

F（x）≤F（0）=f（0）+1=1

即

e-x（f（x）+1）≤1　⇔　f（x）≤ex-1

令G（x）=e-x（1-f（x）），则

G′（x）=e-x（-f′（x）-1+f（x））

由于|f（x）-f′（x）|≤1，所以-f′（x）+f（x）-1≤0，于是G′（x）≤0，即G（x）在［0，+∞）上单调减，因此

G（x）≤G（0）=1-f（0）=1

即

e-x（1-f（x））≤1　⇔　f（x）≥-（ex-1）

于是∀x≥0，有|f（x）|≤ex-1.

例3.45（江苏省2002年竞赛题）　设f（x）在［a，b］上连续，==0，求证：f（x）在（a，b）内至少有两个零点.

解析　方法1　令F（x）=（a≤x≤b），则F（a）=F（b）=0，且F′（x）=f（x）.应用分部积分和积分中值定理，有

这里c∈（a，b），于是F（c）=0.分别在［a，c］与［c，b］上应用罗尔定理，则∃ξ1∈（a，c），∃ξ2∈（c，b），使得F′（ξ1）=F′（ξ2）=0，即f（ξ1）=f（ξ2）=0.于是f（x）在（a，b）内至少有两个零点.

方法2　由积分中值定理，有=f（ξ1）（b-a），a＜ξ1＜b，得f（ξ1）=0.（反证）设f（x）在（a，b）内仅有一个零点ξ1.不妨设a＜x＜ξ1时f（x）＞0，ξ1＜x＜b时f（x）＜0.由条件得

又由于

从而导出了矛盾.故f（x）在（a，b）内至少有两个零点.

例3.46（莫斯科大学1977年竞赛题）　设f（x）在［a，b］上连续，且

求证：f（x）在（a，b）内至少有3个零点.

解析　因f（x）在［a，b］上连续，令F（x）=，则F（a）=F（b）=0，且F′（x）=f（x），应用积分中值定理，∃c∈（a，b），使得

所以F（c）=0.对F（x）在［a，c］与［c，b］上分别应用罗尔定理，∃c1∈（a，c），∃c2∈（c，b），使得

F′（c1）=f（c1）=0，F′（c2）=f（c2）=0

即f（x）在（a，b）内至少有两个零点.

假设f（x）在（a，b）内恰有两个零点c1，c2（a＜c1＜c2＜b），则f（x）取值的符号有下列六种情况：

下面证明这六种情况皆不可能发生.情况1：取多项式p（x）=（x-c1）（xc2）；情况2：取多项式p（x）=c2-x；情况3：取多项式p（x）=c1-x；情况4：取多项式p（x）=（x-c1）（c2-x）；情况5：取多项式p（x）=x-c2；情况6：取多项式p（x）=x-c1.这里多项式为一次或二次多项式，由题意得

另一方面，由于这些多项式在区间（a，c1），（c1，c2），（c2，b）内的取值符号与f（x）在这些区间上的取值符号完全相同，于是在（a，c1），（c1，c2），（c2，b）内p（x）f（x）皆取正值，且p（x）f（x）在［a，b］上连续，所以

从而导出了矛盾.所以f（x）在（a，b）内至少有3个零点.

例3.47（莫斯科全苏大学生1976年竞赛题）　设函数f（x）单调增，∀T＞0，f（x）在［0，T］上可积，且=A，求证：=A.

解析　由=A，可得0＜ε＜1时

利用极限性质可得

由于f（x）单调增，所以

又

对（＊）式应用夹逼准则，得=A.

例3.48（北京市1992年竞赛题）　设f″（x）连续，且f″（x）＞0，f（0）=f′（0）=0，试求极限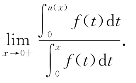

其中u（x）是曲线y=f（x）在点（x，f（x））处的切线在x轴上的截距.

解析　曲线y=f（x）在点（x，f（x））处切线为

Y-f（x）=f′（x）（X-x）

令Y=0，得X=x-，即

应用f（x）与f′（x）的马克劳林公式，有

因此，u（x）=x-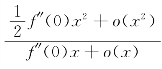，且当x→0时，有

故u（x）=+o（x），且=0.

因此