【摘要】:例3.20(浙江省2007年竞赛题)设求:(1)(1)由于所以(2)由于所以例3.21(南京大学1995年竞赛题)求解析化为定积分计算,有例3.22(江苏省2006年竞赛题)已知f(x)=ax3,求解析化为定积分求极限,则例3.23(莫斯科国民经济学院1976年竞赛题)设f∈C[0,1],f(x)>0,求证:解析应用定积分的定义,有例3.24(莫斯科钢铁与合金学院1976年竞赛题)
例3.20(浙江省2007年竞赛题) 设
求:(1)![]()
(1)由于![]() 所以
所以![]()
(2)由于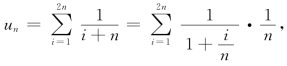 所以
所以
例3.21(南京大学1995年竞赛题) 求
解析 化为定积分计算,有
例3.22(江苏省2006年竞赛题) 已知f(x)=ax3,求
解析 化为定积分求极限,则
例3.23(莫斯科国民经济学院1976年竞赛题) 设f∈C[0,1],f(x)>0,求证:
解析 应用定积分的定义,有
例3.24(莫斯科钢铁与合金学院1976年竞赛题) 求
解析 令
用放缩法,即
由定积分的定义,有
又![]() ,所以
,所以![]()
例3.25(南京大学1996年竞赛题) 已知(https://www.xing528.com)
求f′(0).
解析 当x≠0时,由于![]() ,记t=
,记t=![]() ,则应用重要极限公式可得
,则应用重要极限公式可得
当x=0时,应用定积分求极限,有
于是
故
例3.26(江苏省1996年竞赛题) 设
(1)讨论f(x)在x=0的可导性;
(2)求函数f(x)在[-π,π]上的最大值.
解析 (1)当x>0时
当x=0时
记![]() ,显然1<a<
,显然1<a<![]() .考虑级数
.考虑级数![]() ,因为
,因为
这里bn=![]() 据比值判别法得级数
据比值判别法得级数![]() 收敛,由级数收敛的必要条件得
收敛,由级数收敛的必要条件得
所以f(0)=1.当x<0时f(x)=f(-x)=![]() =
=![]() 故
故
(2)0<x≤π时,f′(x)=![]() ,令g(x)=xcosx-sinx,则g′(x)=-xsinx≤0,且仅当x=π时g′(x)=0,所以g(x)严格减,g(x)<g(0)=0,所以f′(x)<0,f(x)严格减.而f(x)为偶函数,故-π≤x<0时f(x)严格增.因此f(x)在[-π,π]上的最大值为f(0)=1.
,令g(x)=xcosx-sinx,则g′(x)=-xsinx≤0,且仅当x=π时g′(x)=0,所以g(x)严格减,g(x)<g(0)=0,所以f′(x)<0,f(x)严格减.而f(x)为偶函数,故-π≤x<0时f(x)严格增.因此f(x)在[-π,π]上的最大值为f(0)=1.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




