例2.102(莫斯科钢铁与合金学院1977年竞赛题) 求证不等式
解析 不妨设a<b.令
f(x)=(ex+ea)(x-a)-2(ex-ea) (x≥a)
则f(a)=0,而
f′(x)=ex(x-a)+(ex+ea)-2ex=ex(x-a)-(ex-ea)
=ex(x-a)-eξ(x-a)=(ex-eξ)(x-a)
其中a<ξ<x.由于ex>eξ,所以f′(x)≥0⇒x>a时f(x)严格增⇒f(x)>f(a)=0,即当x>a时
(ex+ea)(x-a)>2(ex-ea)
取x=b>a,即得
(eb+ea)(b-a)>2(eb-ea)
此式等价于
例2.103(莫斯科大学数力系1977年竞赛题) 求证不等式
解析 (1)0<x<1时,原式⇔lnx≥![]() 令f(x)=lnx-
令f(x)=lnx-![]() ,则
,则
令g(x)=![]() -x-1,则
-x-1,则![]() >0⇒g(x)↑⇒g(x)<g(1)=0⇒f′(x)<0⇒f(x)↓,故f(x)>f(1)=0,即
>0⇒g(x)↑⇒g(x)<g(1)=0⇒f′(x)<0⇒f(x)↓,故f(x)>f(1)=0,即![]()
(2)x>1时,原式![]() 令
令![]() 则
则
令g1(x)=1+x-![]() ,则
,则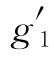 (x)=
(x)=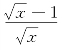 >0⇒g1(x)↑⇒g1(x)>g(1)=0⇒
>0⇒g1(x)↑⇒g1(x)>g(1)=0⇒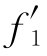 (x)>0⇒f1(x)↑,故f1(x)>f1(1)=0,即lnx≤
(x)>0⇒f1(x)↑,故f1(x)>f1(1)=0,即lnx≤![]()
由(1)和(2),原式得证.
例2.104(浙江省2007年竞赛题) 证明:
解析 令f(x)=![]() ,则
,则
进一步假设g(x)=![]() ,则
,则
当x∈![]() 时g′(x)<0,且g(0)=0,故
时g′(x)<0,且g(0)=0,故
由此,f′(x)=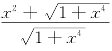 g(x)<0.结合f(0)=1,得
g(x)<0.结合f(0)=1,得
即原不等式成立.
例2.105(江苏省2010年竞赛题) 设a为正常数,使得x2≤eax对一切正数x成立,求常数a的最小值.
解析 根据题意,有
要求a的最小值,只要求f(x)=![]() 的最大值.
的最大值.
令![]() ,得x=e.由于0<x<e时f′(x)>0,x>e时f′(x)<0,所以f(e)=
,得x=e.由于0<x<e时f′(x)>0,x>e时f′(x)<0,所以f(e)=![]() 为其最大值,故a的最小值为
为其最大值,故a的最小值为![]()
例2.106(浙江省2003年竞赛题) 求使得不等式![]() 对所有自然数n都成立的最小的数β.
对所有自然数n都成立的最小的数β.
解析 原不等式等价于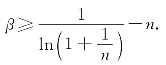 令t=
令t=![]() ,则0<t≤1.令f(t)=
,则0<t≤1.令f(t)=![]() ,问题化为求f(t)的最大值.由于
,问题化为求f(t)的最大值.由于
上式中分母是大于零的,下面来判别分子的符号.令g(t)=(1+t)ln(1+t)-t2(0<t≤1),则
所以曲线g(t)是凸的,g(t)的最小值在其端点取得.由于g(0)=0,g(1)=2ln2-1>0,故当0<t≤1时g(t)>0.因此当0<t≤1时f′(t)>0,所以f(t)在(0,1]上严格增加,因而f(t)≤f(1)=![]() -1,故β=
-1,故β=![]() -1.
-1.
例2.107(江苏省1994年竞赛题) 试比较πe与eπ的大小.
解析 令f(x)=ex-xe(x≥e),则
f′(x)=ex-exe-1
f″(x)=ex-e(e-1)xe-2
f‴(x)=ex-e(e-1)(e-2)xe-3
由于e-3<0,故xe-3单调减(x≥e),-e(e-1)(e-2)xe-3单调增,ex也单调增,于是f‴(x)在x≥e时单调增.x≥e时
f‴(x)≥f‴(e)=ee-e(e-1)(e-2)ee-3
=ee-2(e2-e2+3e-2)
=ee-2(3e-2)>0
故f″(x)严格增.x≥e时
f″(x)≥f″(e)=ee-e(e-1)ee-2=ee-1>0
故f′(x)严格增.x>e时
f′(x)>f′(e)=0
故f(x)严格增.x>e时,f(x)>f(e)=0,取x=π即得f(π)>0,即πe<eπ.
例2.108(精选题) 设f(x)在[0,+∞)上二阶可导,f(0)=1,f′(0)≤1,f″(x)<f(x),求证:x>0时,f(x)<ex.
解析 令F(x)=e-xf(x),则
F′(x)=e-x(f′(x)-f(x))
令G(x)=ex(f′(x)-f(x)),则
G′(x)=ex(f″(x)-f(x))<0
⇒G(x)↓⇒
G(x)<G(0)=f′(0)-f(0)≤0
⇒f′(x)-f(x)<0⇒
F′(x)=e-x(f′(x)-f(x))<0
⇒F(x)↓⇒
F(x)=e-xf(x)<F(0)=1
由此可得f(x)<ex.
例2.109(江苏省1991年竞赛题) 设a1,a2,…,an为常数,且
试证明:![]() (https://www.xing528.com)
(https://www.xing528.com)
解析 令f(x)=a1sinx+a2sin2x+…+ansinnx,则
因为
所以
|a1+2a2+3a3+…+nan|≤1
令g(x)=a1sinnx+a2sin(n-1)x+…+ansinx,则
因为
所以
|na1+(n-1)a2+…+2an-1+an|≤1
综上,有
|(1+n)(a1+a2+…+an)|
=|(a1+na1)+(2a2+(n-1)a2)+…+(nan+an)|
≤|a1+2a2+…+nan|+|na1+(n-1)a2+…+an|
≤1+1=2
于是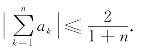
例2.110(江苏省2000年竞赛题) 假设f(x)=a1sinx+a2sin2x+…+ansinnx,其中a1,a2,…,an是实数,且|f(x)|≤|sinx|,试证:
|a1+2a2+…+nan|≤1
解析 方法1 根据题意,有
由题意知x≠0时
由极限的保向性得
由于
于是
|a1+2a2+…+nan|≤1
方法2 由于
又
而
所以
|a1+2a2+…+nan|≤1
例2.111(南京大学1995年竞赛题) 设在[0,2]上定义的函数f(x)∈C(2),且f(a)≥f(a+b),f″(x)≤0,证明:对于0<a<b<a+b<2,恒有
解析 分别在区间[a,b]和[b,a+b]上应用拉格朗日中值定理,∃ξ∈(a,b)和η∈(b,a+b),使得
f(b)-f(a)=f′(ξ)(b-a)
f(a+b)-f(b)=f′(η)(a+b-b)=af′(η)
因为f″(x)≤0,所以f′(x)单调减,故f′(ξ)≥f′(η),即
⇔ a(f(b)-f(a))≥(f(a+b)-f(b))(b-a)
⇔ bf(b)+af(a)≥bf(a+b)+af(a+b)+2a(f(a)-f(a+b))
因为f(a)≥f(a+b),故
bf(b)+af(a)≥(a+b)f(a+b)
即
例2.112(莫斯科国立师范学院1977年竞赛题) 求实数α的取值范围,使得不等式
对一切正数x与y成立.
解析 当α=1时原式化为x≤x,故α=1满足条件.当α≠1时,令
则
若0<α<1,则有
所以f(y)在y=x时有极大值f(x)=x,于是f(y)<x(y≠x).故0<α<1时原不等式不成立.若α<0,则有
所以f(y)在y=x时有极大值f(x)=x,于是f(y)<x(y≠x),故α<0时原不等式不成立.若α>1,则有
所以f(y)在y=x时有极小值f(x)=x,于是∀y∈R有f(y)≥x.即α>1时原不等式成立.故所求的α的取值范围是[1,+∞).
例2.113(北京市1993年竞赛题) 设y>x>0,求证:![]()
解析 分四种情况证明.
(1)当0<x<y≤1时,lnx<lny≤0,则
ylnx<ylny≤xlny⇒0<xy<yx⇒yxlnx<yxlny≤xylny⇒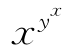 <
<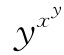
(2)当0<x≤1<y时,lnx≤0<lny,则
yxlnx≤0<xylny⇒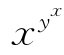 <
<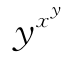
(3)当1<x<y且yx≤xy时,0<lnx<lny,则
yxlnx<yxlny≤xylny⇒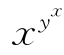 <
<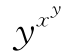
(4)当1<x<y且xy<yx时,0<lnx<lny,ylnx<xlny,且
∀x0>1,令f(y)=ylnx0+lny-x0lny-lnx0(y≥x0),则f(x0)=0,且
于是f′(y)严格增加,f′(y)>f′(x0)=lnx0+![]() -1.令g(x)=lnx+
-1.令g(x)=lnx+![]() -1(x>1),则g′(x)=
-1(x>1),则g′(x)=![]() >0,所以g(x)严格增加,g(x0)>g(1)=0,于是f′(y)>0,f(y)严格增加,则f(y)>f(x0)=0.由x0>1的任意性,得ylnx+lnyxlny-lnx>0,即xyy-yxx>0,又
>0,所以g(x)严格增加,g(x0)>g(1)=0,于是f′(y)>0,f(y)严格增加,则f(y)>f(x0)=0.由x0>1的任意性,得ylnx+lnyxlny-lnx>0,即xyy-yxx>0,又![]() >0,所以
>0,所以
xylny-yxlnx>0⇒ >
>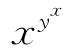
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




