【摘要】：例2.71（江苏省2002年竞赛题）已知，求k和c.解析应用等价无穷小因子代换与洛必达法则，有因为c≠0，所以k-1=2，于是所以k=3，c=.例2.72（南京大学1996年竞赛题）解析令x=，并运用洛必达法则，则例2.73（南京大学1996年竞赛题）求解析化简后应用洛必达法则，有例2.74（江苏省2000年竞赛题）求解析应用洛必达法则，并应用取对数求导法则，有例2.75（精选题）
例2.71（江苏省2002年竞赛题） 已知
，求k和c.
解析 应用等价无穷小因子代换与洛必达法则，有
因为c≠0，所以k-1=2，于是
所以k=3，c=
.
例2.72（南京大学1996年竞赛题） 
解析 令x=
，并运用洛必达法则，则
例2.73（南京大学1996年竞赛题） 求
解析 化简后应用洛必达法则，有
例2.74（江苏省2000年竞赛题） 求
例2.75（精选题） 求
例2.76（江苏省2012年竞赛题） 设f（x）在x=0处3阶可导，且f′（0）=0，
(www.xing528.com)
解析 应用洛必达法则及等价无穷小替换，则
例2.77（南京大学1995年竞赛题） 求
例2.78（全国大学生2010年初赛题） 求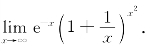
解析 应用洛必达法则，得
注：本题的一个错误解法是
例2.79（浙江省2006年竞赛题） 求
解析 先考虑
应用等价无穷小因子代换与洛必达法则，有
故原式=
例2.80（全国大学生2009年初赛题） 求
其中n是给定的正整数.
解析 利用关于e的重要极限与洛必达法则，得
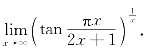
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
