高数竞赛题解析教程：马克劳林公式与泰勒公式应用

例2.50（江苏省2008年竞赛题）　当a=________，b=________时，f（x）=ln（1-ax）+在x→0时关于x的无穷小的阶数最高.

解析　应用马克劳林公式，有

所以

令解得a=1，b=-，此时

所以a=1，b=-时，f（x）在x→0时关于x的无穷小阶数最高（3阶）.

例2.51（江苏省2004年竞赛题）　当x→0时，x-sinxcosxcos2x与cxk为等价无穷小，则c=_________，k=________.

解析　应用三角函数公式化简，有

由于，所以

因x→0时，原式～cxk，所以c=，k=3.

例2.52（南京大学1995年竞赛题）　当x→0时，1-cosxcos2xcos3x对于无穷小x的阶数等于________.

解析　方法1　应用cosx的马克劳林展式，x→0时，有

所以原式的无穷小阶数等于2.

方法2　考虑下列极限

因此式的分子已有极限336，故欲使上式极限C为非零数，仅当k-2=0（即k=2）.此时，即原式为2阶无穷小.

例2.53（莫斯科钢铁与合金学院1976年竞赛题）　设x＞0时，f（x）=（1+，求证：x→0+时，f（x）=e+Ax+Bx2+o（x2），并求A，B之值.

解析　应用ln（1+x）与ex的马克劳林展式，有

例2.54（莫斯科电子技术学院1977年竞赛题）　求

解析　由于x→0时，应用等价无穷小因子代换与马克劳林公式，有

于是

例2.55（全国大学生2012年决赛题）　求

解析

例2.56（北京市1999年竞赛题）　设f（x）具有连续的二阶导数，且

试求

解析　由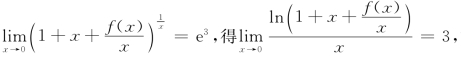故

由此且

故

应用马克劳林公式，x→0时，有

而

例2.57（浙江省2007年竞赛题）　若f（x）二阶可导，且f（x）＞0，f″（x）f（x）-［f′（x）］2＞0，x∈R.（1）证明：f（x1）f（x2）≥∀x1，x2∈R；（2）若f（0）=1，证明：f（x）≥ef′（0）x，∀x∈R.

解析　（1）令F（x）=lnf（x），则

故∀x∈R，F″（x）＞0，于是∀x1，x2∈R，有

即

所以

（2）由马克劳林公式，有

故得

f（x）≥ef′（0）x，∀x∈R

例2.58（全国大学生2011年决赛题）　设函数f（x）在x=0的某邻域内具有二阶连续导数，且f（0），f′（0），f″（0）均不为0，证明：存在惟一一组实数k1，k2，k3，使得

解析　应用f（x）的马克劳林公式

可得

则由

可得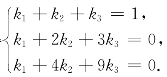应用克莱姆法则，解得惟一解k1=3，k2=-3，k3=1.

例2.59（北京市1990年竞赛题）　设f（x）是一定义于长度等于2^[1]的闭区间I上的实函数，满足|f（x）|≤1，|f″（x）|≤1.对于x∈I，证明：|f′（x）|≤2，且有函数使得等式成立.

解析　假设闭区间I=［a，a+2］，∀x∈I，应用泰勒公式，有

两式相减，得

于是

故得|f′（x）|≤2，x∈I.

考虑函数f（x）=（x-a）2-1，x∈I=［a，a+2］，则|f（x）|≤1，f″（x）=1，且f′（x）=x-a，故|f′（x）|≤2，当x=a+2时，|f′（x）|=2.

例2.60（莫斯科铁路运输工程学院1977年竞赛题）　不查表，求方程

的近似解，精确到0.001.

解析　x≠0时，令u=，应用sinu的马克劳林公式，有

这里0＜θ＜1.于是有

代入原方程得

记因故x＞1976，于是

例2.61（莫斯科铁路运输工程学院1977年竞赛题）　求一函数f（x），使其在任一有限区间上有界，且满足方程

解析　本题是求一函数满足方程，而不是求满足方程的函数.我们可假设函数f（x）任意阶可导，且可展为马克劳林级数.在原式中令x=0可得f（0）=0，原式两边求导得

在（1）式中令x=0得f′（0）=.（1）式两边求导得

在（2）式中令x=0得f″（0）=（2）式两边求导得

在（3）式中令x=0得f‴（0）=0.（3）式两边求导得f（4）（x）=0，如此继续可得

f（n）（x）=0　（n=5，6，…）

因此函数f（x）的马克劳林展式为

此函数f（x）即为所求的函数.

例2.62（北京邮电大学1996年竞赛题）　设函数f（x）在（x0-δ，x0+δ）上有n阶连续导数，且

f（k）（x0）=0　（k=2，3，…，n-1）　且　f（n）（x0）≠0

当0＜|h|＜δ时，有

f（x0+h）-f（x0）=hf′（x0+θh），0＜θ＜1　（＊）

试证：

解析　运用泰勒公式，有

类似有(www.xing528.com)

将两式代入（＊）式并化简可得

故令h→0，则ξ→x0，η→x0，由f（n）（x0）的连续性得

由于f（n）（x0）≠0，故

例2.63（全国大学生2014年决赛题）　设f∈C（4）（-∞，+∞），且

其中θ是与x，h无关的常数，证明：f是不超过3次的多项式.

解析　若f（x）是不超过2次的多项式，因f″（x）≡常数，所以∀θ∈（0，1），（＊）式成立.

下面不妨设f（x）不是不超过2次的多项式.对函数f″（x）应用泰勒公式，在x与x+θh之间必存在ξ，使得

其中θ为0，1之间的常数.将上式代入（＊）式并化简得

此式两边令h→0，并应用洛必达法则，得

由此可得f（4）（x）≡0，于是函数f（x）是3次多项式，且此时

综上可得f（x）是不超过3次的多项式.

例2.64（全国大学生2012年决赛题）　设f（x）在（-∞，+∞）上无穷次可微，并且满足：存在M＞0，使得

|f（k）（x）|≤M　（x∈（-∞，+∞），k=1，2，…）

且满足，求证：在（-∞，+∞）上有f（x）≡0.

解析　首先，由得对函数f（x）在应用拉格朗日中值定理，必∃ξ1（n）∈，使得

应用马克劳林公式，必使得

依此类推，应用马克劳林公式可得，∀k∈N＊，有f（k）（0）=0.∀x0∈R，再应用马克劳林公式，在0与x0之间必存在ξ，使得

由于级数，所以

因此f（x0）=0.由x0∈R的任意性，即得∀x∈R，有f（x）≡0.

例2.65（莫斯科纺织学院1977年竞赛题）　设f（x）在（0，+∞）上二阶可导，存在，当0＜x＜+∞时，|f″（x）|≤1，求证

解析　∀ε＞0，应用泰勒公式，有

这里x＞0，x＜ξ＜x+ε.于是

令x→+∞，得

由ε＞0的任意性得，即

例2.66（莫斯科电子技术学院1977年竞赛题）　设f（x）二阶可导，f（0）=f（1）=0，，求证：

解析　因f∈C［0，1］，由最值定理，f（x）在［0，1］上最小值存在，令

因f（x）在x=C处可导，所以f′（C）=0.函数f（x）在x=C处的泰勒展式为

这里ξ介于C与x之间，在（1）式中分别令x=0与x=1，得

这里0＜ξ1＜C，C＜ξ2＜1.于是有

（1）当

（2）当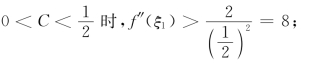

（3）当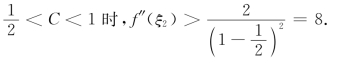

综上，可得

例2.67（江苏省2006年竞赛题）　某人由甲地开汽车出发，沿直线行驶，经过2 h到达乙地停止，一路通畅.若开车的最大速度为100km／h，求证：该汽车在行驶途中加速度的变化率的最小值不大于-200km／h3.

解析　设t为时间，v（t）为速度，a（t）为加速度，则v（0）=0，v（2）=0，设时刻t0速度达最大值，则v（t0）=100，v′（t0）=a（t0）=0.由泰勒公式，有

其中ξ介于t与t0之间.分别令t=0与t=2，得

其中0＜ξ1＜t0＜ξ2＜2.

（1）若t0=1，则a′（ξ1）=a′（ξ2）=-200；

（2）若0＜t0＜1，则

（3）若1＜t0＜2，则

于是

mina′（t）≤min（a′（ξ1），a′（ξ2））≤-200

例2.68（精选题）　设函数f（x）在［a，b］上二阶可导，f′（a）=0，f′（b）=0，求证：∃ξ∈（a，b），使得

解析　函数f（x）在x=a与x=b处的泰勒展式分别为

这里ξ1∈（a，x），η1∈（x，b）.

在（1）和（2）式中分别令得

这里（3）式减（4）式得

这里，且上式即为原式.

例2.69（精选题）　（1）根据ex的两种形式余项的马克劳林展开式

证明：

（2）求证：∃ξ∈（50，100），使得

解析　应用（2）式，有

应用，有

下面证明：当此式成立时，（5）式自然成立.令2x-t=u，则

记f（t）=e-tt　n，则只需证明f（t）＜f（2x-t）（0＜t＜x≤n），即

2（t-x）+nln（2x-t）＞nlnt　（6）

令g（t）=2（t-x）+nln（2x-t）-nlnt（0＜t＜x≤n），则g（x）=0，g′（t）=因为nx≥x2＞2tx-t2，所以g′（t）＜0，从而g（t）严格递减，故g（t）＞g（x）=0，得（6）式成立.

（2）令

则f（t）∈C［50，100］，且

应用介值定理，∃ξ∈（50，100），使得f（ξ）=50.

例2.70（莫斯科大学1977年竞赛题）　设函数f（x）在区间（-1，1）上任意阶可导，且f（n）（0）≠0（n=1，2，3，…），又设对0＜|x|＜1和n∈N，有泰勒公式

这里0＜θ＜1.试求

解析　由题给条件得

于是

由于

故（＊）式两边求极限得

于是