微分中值定理证明题解析

例2.30（莫斯科大学1975年竞赛题）　设f（x）在［0，+∞）上连续可导，f（0）=1，且对一切x≥0有f（x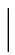）≤e-x，求证：∃ξ∈（0，+∞），使得f′（ξ）=-e-ξ.

解析　令F（x）=f（x）-e-x，则F（x）在（0，+∞）上连续可导，且F（0）=f（0）-1=0.由于|f（x）|≤e-x，所以

于是

若f（x）=e-x，则∀x∈［0，+∞），F（x）=0，于是∀ξ∈（0，+∞），有f′（ξ）=-e-ξ.若f（x）≠e-x，由于|f（x）|≤e-x，所以∃c∈（0，+∞），使得f（c）＜e-c，则F（c）＜0.于是F（x）在（0，+∞）内取得最小值.若F（ξ）是其最小值，则F′（ξ）=0.即∃ξ∈（0，+∞），使得F′（ξ）=0，即f′（ξ）=-e-ξ.

例2.31（精选题）　已知函数f（x）在［a，+∞）上连续，在（a，+∞）上可导，且求证：∃ξ∈（a，+∞），使得f′（ξ）=0.

解析　若∀x≥a有f（x）=f（a），则∀ξ＞a，有f′（ξ）=0.若f（x）≢f（a），则∃b＞a，使得f（b）≠f（a）.不妨设f（b）＞f（a）.记f（b）-f（a）=2ε，ε＞0，在区间［a，b］上应用介值定理，∃c1∈（a，b），使得f（c1）=f（a）+ε.由应用极限的性质，∃N∈（b，+∞），使得

f（a）-ε＜f（N）＜f（a）+ε

在［b，N］上再次应用介值定理，∃c2∈（b，N），使得f（c2）=f（a）+ε.最后在区间［c1，c2］上应用罗尔定理，∃ξ∈（c1，c2）⊂（a，+∞），使得f′（ξ）=0.

例2.32（江苏省2000年竞赛题）　设f（x），g（x）在［a，b］上连续，在（a，b）内可导，且对于（a，b）内的一切x均有f′（x）g（x）-f（x）g′（x）≠0.证明：如果f（x）在（a，b）内有两个零点，则介于这两个零点之间，g（x）至少有一个零点.

解析　（用反证法）假设∀x∈（x1，x2）⊂（a，b），g（x）≠0，这里f（x1）=f（x2）=0.令由于f′（x1）g（x1）-f（x1）g′（x1）=f′（x1）g（x1）≠0，f′（x2）g（x2）-f（x2）g′（x2）=f′（x2）g（x2）≠0，所以g（x1）≠0，g（x2）≠0.于是F（x）在［x1，x2］上可导，且F（x1）=F（x2）=0，应用罗尔定理，必∃ξ∈（x1，x2），使得F′（ξ）=0.由于

所以f′（ξ）g（ξ）-f（ξ）g′（ξ）=0，此与条件∀x∈（a，b），f′（x）g（x）-f（x）g′（x）≠0矛盾.故g（x）在（x1，x2）内至少有一个零点.

例2.33（莫斯科石油与天然气工业学院1976年竞赛题）　设实系数一元n次方程

P（x）=a0xn+a1xn-1+…+an-1x+an=0　（a0≠0，n≥2）

的根全为实数，证明：方程P′（x）=0的根也全为实数.

解析　设方程P（x）=0的n个实根为

c1，c2，…，cr，d1，d2，…，dl

其中c1，c2，…，cr为单根；d1，d2，…，dl为重根，其重数依次为k1，k2，…，kl（kj≥2，j=1，2，…，l），则

r+k1+k2+…+kl=n

对于重根dj（j=1，2，…，l），多项式P（x）可写为

则

由于所以x=dj是方程P′（x）=0的（kj-1）重实根.由此可得方程P′（x）=0有实根d1，d2，…，dl，它们的重数依次为k1-1，k2-1，…，kl-1，这些实根的总个数为

（k1-1）+（k2-1）+…+（kl-1）=n-r-l

另一方面，在P（x）=0的每两个相邻实根之间应用罗尔定理，可得方程P′（x）=0至少有一个实根.由此可得P′（x）=0至少有（r+l-1）个实根.

由上述两种情况获得的方程P′（x）=0的实限，至少有（n-r-l）+（r+l-1）=（n-1）个.而P′（x）=0为实系数一元（n-1）次方程，它至多有（n-1）个实根.因此方程P′（x）=0恰有（n-1）个实根，即P′（x）=0的根全为实数.

例2.34（江苏省2000年竞赛题）　设f（x），g（x）在［a，b］上可微，且g′（x）≠0，证明：存在一点c（a＜c＜b），使得

解析　取辅助函数

F（x）=f（a）g（x）+g（b）f（x）-f（x）g（x）

则F（x）在［a，b］上可微，且F（a）=F（b）=f（a）g（b），应用罗尔定理，∃c∈（a，b），使得F′（c）=0.由于

F′（x）=f（a）g′（x）+g（b）f′（x）-［f′（x）g（x）+f（x）g′（x）］

则

F′（c）=f（a）g′（c）+g（b）f′（c）-［f′（c）g（c）+f（c）g′（c）］=0

化简得

g′（c）（f（a）-f（c））=f′（c）（g（c）-g（b））

由于g′（c）≠0，且g（c）-g（b）≠0（否则∃ξ∈（c，b），使得g′（ξ）=0，此与g′（x）≠0矛盾），所以上式等价于

例2.35（全国大学生2013年决赛题）　设函数f（x）在区间［-2，2］上二阶可导，且|f（x）|≤1，又［f（0）］2+［f′（0）］2=4，试证：在（-2，2）上至少存在一点ξ，使得f（ξ）+f″（ξ）=0.

解析　因为函数f（x）在区间［-2，2］上二阶可导，所以f（x）与f′（x）在区间［-2，2］上皆连续.记F（x）=［f（x）］2+［f′（x）］2，则F（0）=4.

分别在区间［-2，0］与［0，2］上应用拉格朗日中值定理，则存在ξ1∈（-2，0），ξ2∈（0，2），使得

由于|f（x）|≤1，故|f′（ξ1）|≤1，|f′（ξ2）|≤1，得0≤F（ξ1）≤2，0≤F（ξ2）≤2.

因为F（x）在闭区间［ξ1，ξ2］上连续，所以F（x）在［ξ1，ξ2］上取到最大值，设最大值为F（ξ）=M，因F（0）=4，所以M≥4.又因0≤F（ξ1）≤2，0≤F（ξ2）≤2，所以ξ∈（ξ1，ξ2）.因此F（ξ）是F（x）在（ξ1，ξ2）内的极大值，故有F′（ξ）=0，即

F′（ξ）=2f（ξ）f′（ξ）+2f′（ξ）f″（ξ）=2f′（ξ）（f（ξ）+f″（ξ））=0

因为F（ξ）=［f（ξ）］2+［f′（ξ）］2≥4，［f（ξ）］2≤1，所以f′（ξ）≠0，于是有

f（ξ）+f″（ξ）=0

其中ξ∈（ξ1，ξ2）⊂（-2，2）.

例2.36（北京市1992年竞赛题）　设f（x）在［0，π］上连续，在（0，π）内可导，且

求证：∃ξ∈（0，π），使得f′（ξ）=0.

解析　当x∈（0，π）时，有sinx＞0.如果∀x∈（0，π），有f（x）＞0（＜0），则而已知故在（0，π）内f（x）不可能恒正或恒负，即f（x）在（0，π）内必有零点.

假设f（x）在（0，π）内有惟一零点x0，则在（0，x0）及（x0，π）上f（x）异号.不妨设0＜x＜x0时f（x）＞0，x0＜x＜π时f（x）＜0，则

但由已知条件有

导出矛盾，故f（x）在（0，π）内至少存在两个零点x1，x2（x1＜x2）.在区间［x1，x2］上应用罗尔定理，∃ξ∈（x1，x2）⊂（0，π），使f′（ξ）=0.

例2.37（江苏省2004年竞赛题）　设f（x）在［a，b］上连续，在（a，b）内可导，且有求证：在（a，b）内至少有一点ξ，使得

f′（ξ）=f（ξ）-ξ+1

解析　由

对上面的右式应用积分中值定理，∃c∈（a，b），使得

于是f（c）-c=0（a＜c＜b）.取辅助函数

F（x）=e-x（f（x）-x）

则F（a）=F（c）=0，且F（x）在［a，c］上连续，在（a，c）内可导，应用罗尔定理，∃ξ∈（a，c）⊂（a，b），使得F′（ξ）=0.因

F′（x）=e-x（f′（x）-1-f（x）+x）

所以F′（ξ）=e-ξ（f′（ξ）-1-f（ξ）+ξ）=0，即

f′（ξ）=f（ξ）-ξ+1

例2.38（浙江省2004年竞赛题）　已知函数f（x）在［0，1］上三阶可导，且f（0）=-1，f（1）=0，f′（0）=0，试证：至少存在一点ξ∈（0，1），使

解析　令F（t）=f（t）-t2+1-［f（x）-x2+1］，x∈（0，1），则F∈C［0，1］，F∈D（0，1），且F（0）=F（x）=F（1）=0.在［0，x］与［x，1］上分别应用罗尔定理，∃ξ1∈（0，x），ξ2∈（x，1），使得

F′（ξ1）=0，F′（ξ2）=0　且　F′（0）=0

又F′∈C［0，1］，F′∈D（0，1），因此再在［0，ξ1］与［ξ1，ξ2］上分别应用罗尔定理，∃η1∈（0，ξ1），η2∈（ξ1，ξ2），使得

F″（η1）=0，F″（η2）=0

因F″∈C［0，1］，F″∈D（0，1），再在［η2，η2］上应用罗尔定理知，∃ξ∈（η2，η2）⊂（0，1）使F‴（ξ）=0，而故∃ξ∈（0，1），使

例2.39（南京大学1995年竞赛题）　设f（x）在（0，1）内有三阶导数，0＜a＜b＜1，证明：存在ξ∈（a，b），使得

解析　令

则有恒等式

取辅助函数

由（＊）式得F（b）=0，又F（x）在（0，1）内可导，F（a）=0，在［a，b］上应用罗尔定理，必∃η∈（a，b），使得F′（η）=0.由于

所以F′（a）=0.由于F′（x）在（0，1）上可导，且F′（a）=F′（η）=0，对函数F′（x）在［a，η］上应用罗尔定理，必∃ξ∈（a，η）⊂（a，b），使得又因为

所以

于是k=f‴（ξ），代入（＊）式即为所求证的等式.

例2.40（北京市1996年竞赛题）　考察函数

在闭区间［-4，1］上是否满足拉格朗日中值定理的条件.若满足，求出该定理结论中ξ的值.

解析　由于

故f（x）在x=0处连续，从而f（x）∈C［-4，1］.又

故f（x）在x=0处可导，从而f（x）∈D（-4，1）.由此f（x）在［-4，1］上满足拉格朗日中值定理的条件，且有

根据拉格朗日中值定理，∃ξ∈（-4，1），满足(https://www.xing528.com)

令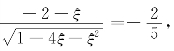则经检验ξ1，2∈（-4，0）；令则经检验ξ3，4∉［0，1）.因此，满足拉格朗日中值定理条件的

例2.41（精选题）　设f（x）在［a，b］上连续，在（a，b）内可导，且f（a）=0，f（b）=1，求证：∃ξ∈（a，b），η∈（a，b），ξ≠η，使得

解析　首先应用介值定理，可知∃c∈（a，b），使得f（c）=.在区间［a，c］与［c，b］上分别应用拉格朗日中值定理，可知∃ξ∈（a，c）⊂（a，b），η∈（c，b）⊂（a，b），且ξ≠η，使得

f（c）-f（a）=f′（ξ）（c-a），f（b）-f（c）=f′（η）（b-c）

即有

故

例2.42（精选题）　设f（x）在［0，1］上连续，在（0，1）内可导，且有f（0）=0，f（1）=1，若a＞0，b＞0，求证：∃ξ∈（0，1），η∈（0，1），ξ≠η，使得

解析　∀k∈（0，1），应用介值定理，∃c∈（0，1），使得f（c）=k.在［0，c］与［c，1］上分别应用拉格朗日中值定理，∃ξ∈（0，c）⊂（0，1），η∈（c，1）⊂（0，1），且ξ≠η，使得

f（c）-f（0）=f′（ξ）（c-0）

f（1）-f（c）=f′（η）（1-c）

即

取则代入上式即得

例2.43（精选题）　设f（x）在（0，+∞）上可导.

（1）若，求证：

（2）若，求

解析　（1）因为f′（x）→k（x→+∞），所以∃N＞0，当x＞N时，f′（x）＞＞0.在［N，x］（x＞N）上应用拉格朗日中值定理，∃ξ∈（N，x），使得

令x→+∞，得

（2）取k∈R，使得k+l＞0，则

由（1）得

例2.44（全国大学生2013年决赛题）　设函数f（x）在区间［1，+∞）上连续可导，且

证明：存在.

解析　当x≥1时，对于函数lnx，在区间［x，x+1］上应用拉格朗日中值定理，存在ξ∈（x，x+1），使得

由此可得，因此又0，所以f′（x）＞0，于是x≥1时函数f（x）严格增.又因为

上式两边从1到x积分得

即

所以函数f（x）有上界.综上，应用单调有界准则即得存在.

例2.45（精选题）　当x≥0时，求证：∃θ（x）∈（0，1），使得

并求

解析　设f（t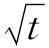）=，对函数f（t）在区间［x，x+1］上应用拉格朗日中值定理，∃θ（x）∈（0，1），使得

f（x+1）-f（x）=f′（ξ）（x+1-x）

其中ξ=x+θ（x）·1=x+θ（x），即

由上式解得

于是

例2.46（全国大学生2010年初赛题）　设函数f（x）在（-∞，+∞）上具有二阶导数，并且且存在一点x0使得f（x0）＜0，证明：方程f（x）=0在（-∞，+∞）上恰有两个实根.

解析　由f″（x）＞0，可得f′（x）在（-∞，+∞）上严格增加；由α＞0可得，存在b＞0使得f′（b）＞0；由可得，存在a＜0使得f′（a）＜0.由于f′（x）在闭区间［a，b］上连续，应用零点定理，∃ξ∈（a，b），使得f′（ξ）=0，且当x＜ξ时，f′（x）＜0；当x＞ξ时，f′（x）＞0.由于f″（ξ）＞0，所以f（ξ）是函数f（x）的极小值.因为f（x0）＜0，所以f（ξ）＜0.

任取x＞ξ，应用拉格朗日中值定理，∃ξ1∈（ξ，x），使得

f（x）=f（ξ）+f′（ξ1）（x-ξ）　（其中f′（ξ1）＞0）

由此式可得，因此∃d∈（ξ，+∞），使得f（d）＞0.

任取x＜ξ，应用拉格朗日中值定理，∃ξ2∈（x，ξ），使得

f（x）=f（ξ）+f′（ξ2）（x-ξ）　（其中f′（ξ2）＜0）

由此式可得=+∞，因此∃c∈（-∞，ξ），使得f（c）＞0.

因为f（c）＞0，f（ξ）＜0，f（d）＞0，f（x）分别在闭区间［c，ξ］与［ξ，d］上连续，应用零点定理，∃η∈（c，ξ），ζ∈（ξ，d），使得f（η）=f（ζ）=0.

因为x＜ξ时f′（x）＜0，x＞ξ时f′（x）＞0，所以函数f（x）在区间（-∞，ξ］上严格减少，在区间［ξ，+∞）上严格增加，故f（x）在区间（-∞，ξ）内至多有一个零点，在区间（ξ，+∞）内也至多有一个零点，因此方程f（x）=0在（-∞，+∞）上恰有两个实根.

例2.47（莫斯科钢铁与合金学院1975年竞赛题）　设f（x）在（0，+∞）上连续可导，存在，f（x）的图形在（0，+∞）上是凸的，求证：

解析　设=A，令F（x）=f（x）-A，则

由于f（x）在（0，+∞）上是凸的⇔f′（x）在（0，+∞）严格减，因此F′（x）=f′（x）在（0，+∞）上严格减.

∀c＞0，若F′（c）＜0，在［c，x］上应用拉格朗日中值定理，∃ξ∈（c，x）使得

F（x）=F（c）+F′（ξ）（x-c）＜F（c）+F′（c）（x-c）

令x→+∞得，此与F（+∞）=0矛盾.故∀x∈（0，+∞），有F′（x）≥0.于是x→+∞时，F′（x）严格减，有下界，应用单调有界准则得x→+∞时F′（x）的极限存在，且=B≥0.若B＞0，在区间［1，x］上应用拉格朗日中值定理，∃η∈（1，x），使得

F（x）=F（1）+F′（η）（x-1）＞F（1）+B（x-1）

令x→+∞得=+∞，此与F（+∞）=0矛盾.所以B=0，即

解析　在|f′（x）|≤k|f（x）|中取x=0，可得f′（0）=0.∀x∈（0，1），应用拉格朗日中值定理，∃ξ1∈（0，x）⊂（0，1），使得

f（x）=f（0）+f′（ξ1）x=f′（ξ1）x

于是

|f（x）|=|f′（ξ1）|x≤k|f（ξ1）|x　（1）

在［0，ξ1］上再应用拉格朗日中值定理，∃ξ2∈（0，ξ1），使得

f（ξ1）=f（0）+f′（ξ2）ξ1=f′（ξ2）ξ1

于是|f（ξ1）|=|f′（ξ2）|ξ1≤k|f（ξ2）|x，代入（1）式得

|f（x）|≤k2|f（ξ2）|x2　（2）

再在［0，ξ2］上应用拉格朗日中值定理，∃ξ3∈（0，ξ2），使得

|f（x）|≤k3|f（ξ3）|x3　（3）

如此继续下去，∃ξn∈（0，ξn-1），使得

|f（x）|≤kn|f（ξn）|xn　（4）

由于f（x）在［0，1］上连续，必有界，即∃M＞0，使得|f（ξn）|≤M（n=1，2，…），而0＜k＜1，0＜x＜1，在（4）式右端令n→∞得

于是f（x）≡0，0≤x＜1.再由f∈C［0，1］，得

即f（1）=0.于是f（x）≡0，x∈［0，1］.

例2.49（莫斯科大学1975年竞赛题）　设f（x）在（-∞，+∞）上有界，且二阶可导，求证：∃ξ∈R，使得f″（ξ）=0.

解析　（1）若∃a，b∈（-∞，+∞），且a＜b，使得f′（a）=f′（b），令F（x）=f′（x），则函数F（x）在［a，b］上可导，且有F（a）=F（b），应用罗尔定理，必∃ξ∈（a，b），使得F′（ξ）=0，即f″（ξ）=0.

（2）若∀a，b∈（-∞，+∞），且a＜b，f′（a）≠f′（b），则f′（x）在（-∞，+∞）上严格增或严格减.不妨设f′（x）在（-∞，+∞）上严格增.

∀c∈（-∞，+∞），①若f′（c）≥0，则f′（1+c）＞0，当x＞1+c时，在［1+c，x］上应用拉格朗日中值定理，有

f（x）=f（1+c）+f′（ξ）（x-1-c）

＞f（1+c）+f′（1+c）（x-1-c）

这里1+c＜ξ＜x.令x→+∞得=+∞，此与f（x）在（-∞，+∞）上有界矛盾.②若f′（c）＜0，当x＜c时，在［x，c］上应用拉格朗日中值定理，有

f（x）=f（c）+f′（η）（x-c）

＞f（c）+f′（c）（x-c）

这里x＜η＜c.令x→-∞得=+∞，此与f（x）在（-∞，+∞）上有界矛盾.此表明情况（2）不可能发生，只有第（1）种情况发生.