例2.16（南京大学1995年竞赛题） 设f′（0）=1，f″（0）=0，求证：在x=0处，有
解析 应用复合函数的链锁法则，有
所以
=2f′（0）+0=2.而
所以
=2（f′（0））2+2f（0）f″（0）=2.得证.
例2.17（江苏省2006年竞赛题） 设x=ln（1+t2），y=arctant，求
解析 应用参数式函数求导公式，有
故
例2.18（全国大学生2009年初赛题） 设y=y（x）由方程xef（y）=eyln29确定，其中f具有二阶导数，且f′≠1，则
解析 显见x＞0，原式两边取对数得
lnx+f（y）=y+lnln29
两边对x求导数得
由（＊）式可得
（＊）式两边对x再求导数得
由此式解出y″，并利用y′的表达式可得
例2.19（江苏省2000年竞赛题） 若y=y（x）由方程组
确定，求
解析 由x=t2-t，x′（t）=2t-1，x″（t）=2，所以x′（0）=-1，x″（0）=2.设由tey+y+1=0确定y=y（t），则y（0）=-1.方程两边对t求导得
ey+tey·y′（t）+y′（t）=0 （＊）
令t=0得e-1+0+y′（0）=0，所以y′（0）=
（＊）式两边求t求导数得
2eyy′（t）+tey（y′（t））2+teyy″（t）+y″（t）=0
令t=0得2e-1y′（0）+0+0+y″（0）=0，所以y″（0）=
于是
例2.20（江苏省1994年竞赛题） 设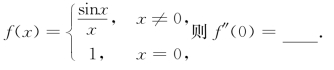
解析 由导数的定义，有
当x≠0时，
再用定义求f″（0）得
例2.21（南京大学1996年竞赛题） 已知f（x）=cos2x，求f（2n）（0）.
解析 由于
，所以
例2.22（南京大学1996年竞赛题） 已知
，求f（n）（3）.
解析 将f（x）分解为部分分式，即
由公式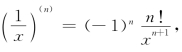
可得
令x=3，得(www.xing528.com)
例2.23（江苏省1991年竞赛题） 设
其中m，n为正整数，则P（1）=________.
解析 因为
（1-xm）n=（1-x）n·（1+x+x2+…+xm-1）n
令u（x）=（1-x）n，v（x）=（1+x+…+xm-1）n，应用莱布尼兹公式，因u（1）=u′（1）=…=u（n-1）（1）=0，u（n）（1）=（-1）nn！，所以
P（1）=v（n）（1）u（1）+nv（n-1）（1）u′（1）+…+v（1）u（n）（1）
=0+0+…+0+mn（-1）nn！=（-1）nmn·n！
例2.24（江苏省1994年竞赛题） 设f（x）=（x2-3x+2）ncos
，求f（n）（2）.
解析 由f（x）=（x-2）n（x-1）ncos
，令u（x）=（x-2）n，v（x）=（x-1）ncos
，由于u（2）=u′（2）=…=u（n-1）（2）=0，u（n）（2）=n！，应用莱布尼兹公式得
例2.25（广东省1991年竞赛题） 设
，求f（n）（x）.
解析 应用多项式除法，有
由于
所以
例2.26（江苏省2012年竞赛题） 设y=ln（1-x2），求y（n）.
解析 由于
故
例2.27（浙江省2004年竞赛题） 设
求f（n）（0）.
解析 已知
即（1+x2）f′（x）=-1.等式两边对x求（n-1）阶导数，应用莱布尼兹公式，得
令x=0，得
而
故f′（0）=-1，f″（0）=0.所以当n为偶数时，f（n）（0）=0；当n为奇数时，
！.即
例2.28（精选题） 设
求y（n）（0）.
解析 由
令x=0，得y（n+1）（0）=n2y（n-1）（0）.由于y′（0）=1，y″（0）=y（0）=0，所以
y（2n）（0）=0，y（2n+1）（0）=4n（n！）2
例2.29（南京大学1996年竞赛题） 设y=xn-1lnx，求y（n）.
解析 由
归纳假设
则
所以（＊）k+1成立，于是（＊）k对∀k=1，2，…，n-1成立.当k=n-1时
于是
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
