高数竞赛题解析:求导法则解题

例2.8（江苏省2008年竞赛题）　已知f（x）=x（x-1）（x-2）…（x-100），则f′（50）=________.

解析　因为

f′（x）=（x-1）（x-2）…（x-100）+x（x-2）…（x-100）+…

+x（x-1）…（x-48）（x-50）…（x-100）

+x（x-1）…（x-49）（x-51）…（x-100）

+x（x-1）…（x-50）（x-52）…（x-100）+…

+x（x-1）…（x-99）

所以

f′（50）=50·49·…·1·（-1）·（-2）·…·（-50）

=（-1）50（50！）2=（50！）2

例2.9（江苏省1996年竞赛题）　若f（x）=x（2x-1）（3x-2）…（100x-99），则f′（0）=________.

解析　记u（x）=x，v（x）=（2x-1）（3x-2）…（100x-99），则f（x）=u（x）v（x）.因u′（0）=1，u（0）=0，v（0）=-99！，所以

f′（0）=u′（0）v（0）+u（0）v′（0）=-99！

例2.10（北京市1993年竞赛题）　设函数f（u）在-∞＜u＜+∞内可导，且f（0）=0，又

求出f（u）（-∞＜u＜+∞）的表达式.

解析　令lnx=u，则

积分得

由于f（0）=0，所以c1=0，c2=-2，于是

例2.11（江苏省1996年竞赛题）　设当x=0时f′（0）≠0，则f（0）=________.

解析　应用复合函数求导法则，有

令x=0，得f′（0）=2f（0）f′（0）.因f′（0）≠0，所以f（0）=

例2.12（浙江省2003年竞赛题）　求

解析　应用二项式定理，有

两边求导得

两边乘以x后再求导得

令x=1得(www.xing528.com)

化简得于是

例2.13（莫斯科建筑工程学院1997年竞赛题）　设f（x）在（-∞，+∞）上可导.若f（x）为奇函数，求证f′（x）为偶函数；若f（x）为偶函数，求证f′（x）为奇函数.此命题的逆命题是否正确？

解析　因

f（-x）=-f（x）⇒-f′（-x）=-f′（x）⇒f′（-x）=f′（x）

f（-x）=f（x）⇒-f′（-x）=f′（x）⇒f′（-x）=-f′（x）

所以奇函数的导函数为偶函数，偶函数的导函数为奇函数.

但偶函数的原函数不一定为奇函数.例如（1+sinx）′=cosx，这里偶函数cosx的原函数1+sinx并非奇函数.奇函数f（x）的原函数可写为

由于

故奇函数的原函数一定为偶函数.

例2.14（江苏省1998年竞赛题）　函数f（x）=（x2+3x+2）|x3-x|的不可导点的个数为___________.

解析　令u（x）=x2+3x+2，v（x）=|x3-x|，则u（x）处处可导，而v（x）在x=-1，0，1处不可导，在其他点处处可导.u（-1）=0，u（0）=2，u（1）=6.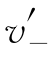（-1）=-2，（-1）=2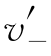；（0）=-1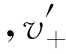（0）=1；（1）=-2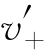，（1）=2.因f（x）=u（x）v（x），又因为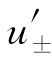（x）=u′（x），则

（x）=u′（x）v（x）+u（x）（x），x）=u′（x）v（x）+u（x）（x）

令x=-1，0，1分别代入上式得

所以f（x）在x=-1处可导，f′（-1）=0.f（x）在x=0和x=1处左、右导数不相等，所以f（x）在x=0与x=1处不可导，其他点处处可导.于是f（x）有2个不可导点.

例2.15（南京大学1996年竞赛题）　证明：两条心脏线ρ=a（1+cosθ）与ρ=a（1-cosθ）在交点处的切线互相垂直.

解析　曲线ρ=a（1+cosθ）化为参数方程为

x=a（1+cosθ）cosθ，y=a（1+cosθ）sinθ

其斜率为

曲线ρ=a（1-cosθ）化为参数方程为

x=a（1-cosθ）cosθ，y=a（1-cosθ）sinθ

其斜率为

再求两曲线的交点.由解得cosθ=0，于是交点的极坐标为

在，因为k1k2=-1，所以两曲线在交点处的切线互相垂直.

在，因为k1k2=-1，所以两曲线在交点处的切线互相垂直.