证明题利用介值定理解析

例1.50（浙江省2011年竞赛题）　证明：［x3］+x2=［x2］+x3存在一个非整数解，其中［x］表示不大于x的最大整数.

解析　令

f（x）=x3-x2+［x2］-［x3］

由于时，［x2］=2，［x3］=3，于是

f（x）=x3-x2+2-3=x3-x2-1

显见f（x）在上连续.由于

应用零点定理，必，使得f（ξ）=0.由于故ξ∈（1，2），即f（x）=0至少有一个非整数解，于是［x3］+x2=［x2］+x3至少存在一个非整数解.

例1.51（北京市1992年竞赛题）　已知

求证：（1）对于任何自然数n，方程在区间中仅有一根；

（2）设满足

解析　（1）已知且0，则由介值定理知，对于存在，使得又

因此fn（x）在上严格递减，故xn是惟一存在的.

（2）由，得

故存在正整数N，当n＞N时，有

由于fn（x）严格递减，所以令n→∞，则，应用夹逼准则可得

例1.52（浙江省2008年竞赛题）　（1）证明fn（x）=xn+nx-2（n为正整数）在（0，+∞）上有惟一正根an；（2）计算

解析　（1）由于fn（0）=-2＜0，，故在上应用零点定理，，使fn（an）=0.又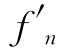（x）=nxn-1+n＞0，x∈（0，+∞），即fn（x）在（0，+∞）上严格单调增，故在（0，+∞）上有惟一正根an.(www.xing528.com)

（2）由n∈N＊得故

进一步得，因此

令n→∞，则

应用夹逼准则知

例1.53（北京市1994年竞赛题）　设fn（x）=x+x2+…+xn（n=2，3，…）.证明：（1）方程fn（x）=1在［0，+∞）内有惟一的实根xn；（2）求

解析　（1）由题可知fn（x）在［0，1］上连续，且fn（0）=0，fn（1）=n＞1.由介值定理知，∃xn∈（0，1），使得fn（xn）=1.又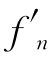（x）=1+2x+…+nxn-1＞0，x≥0，即fn（x）在［0，+∞）上严格递增，故fn（x）=1在［0，+∞）内有惟一的实根xn.

（2）由（1）知，∀n≥2，有0＜xn＜1，故数列｛xn｝是有界的.又fn（xn）=1=fn+1（xn+1），即

移项得

故xn＞xn+1，即数列｛xn｝单调减少.据单调有界准则知数列｛xn｝收敛.

由，应用夹逼准则，得.又

令xn→A（n→∞），则.解得，所以

例1.54（精选题）　已知函数f（x）在闭区间［a，b］上连续，且f（a）=f（b），求证：∃ξ∈（a，b），使得

解析　令则

由此可得

（1）当

（2）当时，应用零点定理，，使得F（ξ）=0，即