高等数学竞赛：夹逼法与单调有界法求极限

例1.19（江苏省2006年竞赛题）　求

解析　利用夹逼准则，令，由于

又

所以

例1.20（南京大学1995年竞赛题）　求

解析　由于，当x＞0时

由左边不等式推知≤1，由右边不等式推知1，所以

当x＜0时

由左边不等式推知≤1，由右边不等式推知1，所以

因而

例1.21（南京工业大学2009年竞赛题）　求

解　原式，由于

因为→0，由夹逼准则得，故原式=1+0=1.

例1.22（浙江省2007年竞赛题）　求

解析　

令

则

由于

故

又因为2≤k＜n时

所以

又

由于

故

又因为2≤k＜n时

所以

于是∀n∈｛2，3，…｝，有0＜xn＜3，故

应用夹逼准则，得

例1.23（江苏省2008年竞赛题）　设数列｛xn｝为x1=1，xn+1=（n=1，2，…），求证数列｛xn｝收敛，并求其极限.

解析　因为，归纳假设0＜xn-1＜xn⇒0＜6+xn-1＜6+xn⇒xn=所以数列｛xn｝单调增.又x1＜3，归纳假设xn＜3⇒xn+1==3，所以数列｛xn｝有上界3，应用单调有界准则得数列｛xn｝收敛.

令xn→A，则xn+1→A⇒A=⇒A=3，于是

例1.24（江苏省2008年竞赛题）　设数列｛xn｝为，求证数列｛xn｝收敛，并求其极根.

解析　因为

所以(www.xing528.com)

由于应用夹逼准则得x2n→1，x2n+1→1，故

例1.25（莫斯科动力学院1975年竞赛题）　设x1=b，xn+1=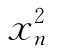+（1-2a）xn+a2（n≥1），当a，b满足何条件时数列｛xn｝收敛？并求

解析　因为xn+1=xn+（xn-a）2，于是xn+1≥xn，即xn单调增.若｛xn｝收敛，令xn→A⇒A=a.由

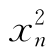+（1-2a）xn+a2≤a⇒a-1≤xn≤a

则a-1≤b≤a.

反之，设a-1≤b≤a，则

xn+1≥xn≥a-1，xn+1=xn+（xn-a）2≤xn+a-xn=a

故｛xn｝单调增，有上界a.

于是a-1≤b≤a，且

例1.26（莫斯科轻工业学院1977年竞赛题）　求正整数n，使得

n＜6（1-1.001-1000）＜n+1

解析　由于数列单调增加且趋向于e，所以又取n=1000，得

于是所求正整数n=3.

例1.27（莫斯科公路学院1976年竞赛题）　设a＞b＞0，定义数列求证：这两个数列皆收敛，且其极限相等.

解析　由于

所以0＜b＜b1＜a1＜a.同理可得0＜b1＜b2＜a2＜a1，0＜b2＜b3＜a3＜a2.

归纳假设0＜bn-1＜bn＜an＜an-1，则

所以0＜bn＜bn+1＜an+1＜an，由此得数列｛an｝单调减，有下界b；数列｛bn｝单调增，有上界a.应用单调有界准则，它们皆收敛.设

在两边令n→∞，得

2A=A+B，B2=AB

由于A＞0，B＞0，所以A=B，即

例1.28（莫斯科技术物理学院1976年竞赛题）　设，求证：数列｛cn｝收敛于AB，其中

解析　由题给条件得

an=A+αn，bn=B+βn

这里αn→0，βn→0（n→∞）.于是

由于αn→0，所以∀ε＞0，∃N∈N，当n＞N时，且

另一方面，由于，所以∀ε＞0，∃M∈N，当n＞M时，故∀ε＞0，取K=max｛N，M｝，则当n＞K时，有

由极限的定义得（α1+α2+…+αn）→0（n→∞），于是

同理可得βn→0时，有

由于αn→0，所以∃k＞0，使得∀n∈N，有|αn|＜k，于是

由于βn→0时

所以

综上，在（＊）式中令n→∞，即得