Python循环结构实例

【例3-18】编写程序,随机产生一个1～100范围内的整数,给用户三次猜测机会,程序给出猜测提示(偏大或偏小)。如果某次猜测正确,则提示正确并中断循环;如果三次均猜错,则提示机会用完。

分析:使用随机函数产生随机整数,设置循环初值为1,循环次数为3,在循环体中输入猜测并进行判断,如果密码正确则使用break语句中断当前循环。

程序如下:

程序运行过程如图3-43～图3-46所示。

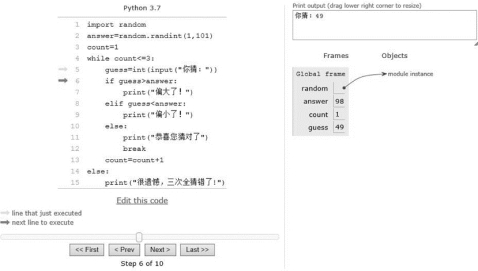
图3-43　程序运行过程1

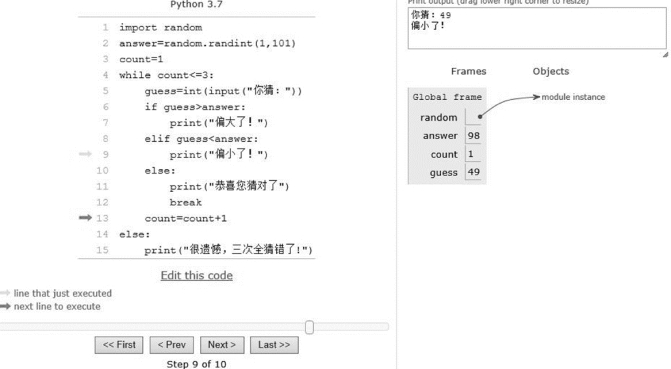
图3-44　程序运行过程2

图3-45　程序运行过程3

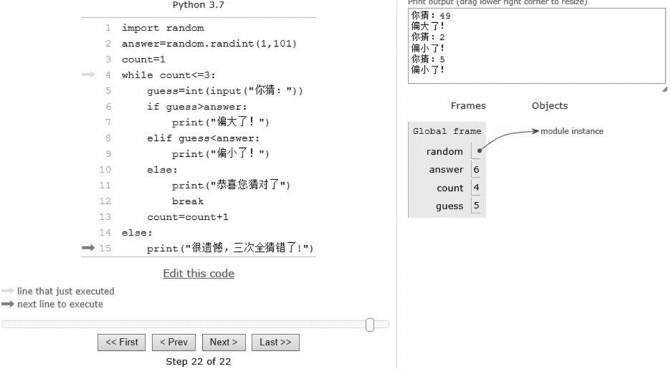
图3-46　程序运行过程4

【例3-19】求a、b两个数的最大公约数。

分析1:设b为两数中较小的一个,则最大公约数必在1与b的范围内。用for循环,循环变量i从b变化到1,如果i同时被a与b整除,则i是最大公约数,退出循环。如果最大公约数是1,那么两个数是互质数。

程序如下:

程序的运行结果如下:

程序运行过程如图3-47～图3-49所示。

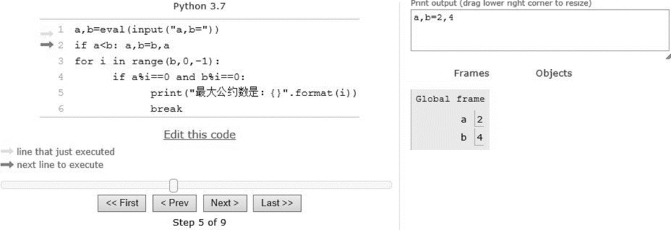
图3-47　程序运行过程1

图3-48　程序运行过程2

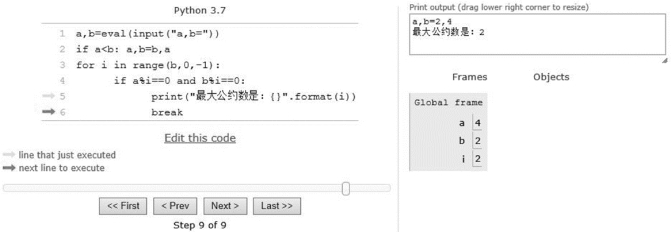
图3-49　程序运行过程3

分析2:最大公约数的步骤如下。

(1)计算两个数a和b的余数r;

(2)如果余数r不为0,则以b和r作为新的a和b,回到(1),重复计算;(www.xing528.com)

(3)否则b就是余数。

比如两个数60和18,第一次60/18余6,第二次18/6余0,于是最大公约数就是6。

程序如下:

思考:以上两种方法哪种效率更高?

【例3-20】求100～200的全部素数及数量。

分析:【例3-17】中可以判断一个数是否是素数,本例要求100～200的所有素数,可以加一层循环,用于提供要判断的数100,101,…,200。k用于计数,控制每输出10个数换行。

程序如下:

程序的运行结果如下:

程序运行过程如图3-50～图3-52所示。

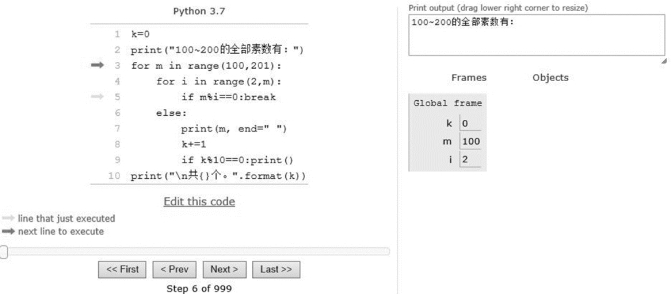
图3-50　程序运行过程1

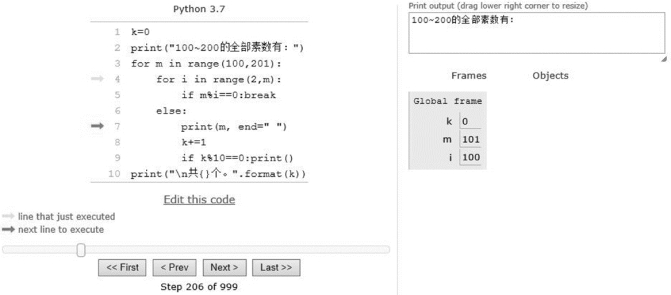
图3-51　程序运行过程2

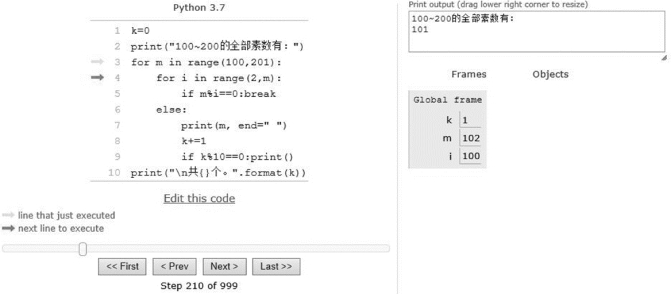
图3-52　程序运行过程3

【例3-21】“百钱百鸡”问题。公鸡5文钱一只,母鸡3文钱一只,小鸡3只一文钱,用100文钱买100只鸡,其中公鸡、母鸡、小鸡都必须要有,问公鸡、母鸡、小鸡要买多少只刚好凑足100文钱?

分析1:这是一个组合问题,也可以看作是解不定方程的问题,采用列举的方法实现。令i、j、k分别表示公鸡、母鸡和小鸡的数目。根据本例的要求,公鸡最多能买20只,i取值1～20;母鸡最多能买33只,j取值1～33;小鸡最多能买100只,k取值1～100。采用三重循环逐个搜索。

程序如下:

程序运行结果如下:

分析2:在保证每种鸡至少买一只的前提下,i、j、k的列举范围进一步修改,公鸡最多能买20只,i取值1～20;母鸡最多能买33只,j取值1～33;当公鸡、母鸡的数量确定后,小鸡的数量可以计算得到,k=100-i-j。采用双循环逐个搜索。

程序如下:

思考:两种方法下,循环体被执行的次数各是多少?