非线性光学与光子学中密度矩阵方程的求解法

为对有阻尼情况下的密度矩阵方程式（18-6）进行逐次求解，首先应把外电磁场与组成介质的粒子体系的作用，理解为一组不同的单色平面光波的特定组合与粒子之间的相互作用。在激光入射作用的情况下，光场常表现为数目有限的单色波的组合，在此情况下总光场可简单表为如下的傅里叶级数的形式：

按照通常的假设，设所考虑的介质子系综的线度远小于光波长，故场的空间变化可忽略。进一步假设光波长更是远大于介质粒子本身的线度，则可采用电偶极矩近似，而将相互作用哈密顿算符写为傅里叶级数的形式：

与此相应，将各阶密度矩阵分量亦表示为傅里叶级数的形式：

为求解上式，首先将式（18-28）以及

代入式（18-6）中第一个方程可得

然后，以粒子体系的非微扰本征函数系为表象对方程左右两端各项，进行求矩阵元运算，并利用如下的中间运算结果和假设：

上列各式中，Ea和Eb为粒子系统的非微扰本征能量值，ωab=（Ea-Eb）/为从能级a向能级b的跃迁频率，和代表零阶密度矩阵的不同对角矩阵元，Γab为唯象引入的与密度矩阵非对角矩阵元对应的阻尼因子。由此可求得一阶密度矩阵傅里叶分量矩阵元满足的方程式为

从而可解出

式中，

为进一步求出第二阶密度矩阵方程的解，将表达式：

代入式（18-6）第二个方程，然后对各项进行求矩阵元运算可得(www.xing528.com)

考虑入射光场中包含有两种不同频率单色光的情况，此时哈密顿算符可写为

将上式以及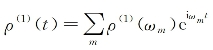同时代入方程式（18-32）可得

以下的分析将表明，二阶密度矩阵可用来描述二阶非线性混频效应。以和频效应为例，令上述方程两端含相同频率组分的傅里叶分量相等，并只考虑和频项贡献则有

利用算符之积求矩阵元的运算公式

并将ρ（1）（ω1）和ρ（1）（ω2）的矩阵元解式（18-31）代入式（18-33）后，可最终求得表示和频过程的二阶密度矩阵元的解为

式中有Dab（ω1+ω2）=（ωba-ω1-ω2-iΓab）以及Dcb（ω2）=（ωbc-ω2-iΓcb）等；而a，b，c为粒子体系不同本征能态的标号。采用一种新的运算操作标记，式（18-34）可进一步化简为

式中，引入的标记是表示在其后的各项中ω1与ω2位置互换后组成的新的各项进行相加。

通过完全相类似的过程，同样可求出描述3种频率的单色波同时入射产生（ω1+ω2+ω3）和频辐射过程的三阶密度矩阵元的解为

式中，第一个求和运算符号表示其后的各项中，ω1，ω2，ω3之间的位置相互任意对调以后所组成的新的各项再相加求和。通过同样的过程，亦可逐次求出更高阶的密度矩阵元之解。不过，一般情况下求到三阶解已足够了。