强太赫兹脉冲通过泡克耳斯效应引起的非线性相位调制

当一束强激光脉冲通过非线性介质时，可经由三阶或二阶非线性过程而在介质内引起折射率的感应变化，与此相关的现象分别称为克尔（Kerr）效应或泡克耳斯（Pockels）效应。对前一效应，折射率变化与光强成正比；对后一效应，折射率变化与光场的振幅成正比（参见第5章）。这种感应折射率随时间的变化，可反过来导致入射激光所经受的自相位调制效应；而感应折射率随空间的变化，还可导致激光束的自聚焦或自散焦效应（参见第6章）。在有一强和一弱两激光束同时入射的情况下，由其中强光束在非线性介质内引起的折射率变化，可以按一定方式被弱光束探测到。进而，可把这种考虑推广到一束强太赫兹辐射与一束弱探测光束同时入射的情况，则前者在非线性介质内引起的折射率变化，亦可对后者产生（互）相位调制的或自聚（散）焦影响。

首先，考虑如图17-9所示双束波场同时重合入射到一种非线性介质的情况，其中一个是单周期强太赫兹脉冲波场，另一个是时宽要窄得多的频率为ω的弱探测激光脉冲场。在假设前者频率远小于后者的前提下，介质内感应电极化（忽略其矢量特性）可表示为

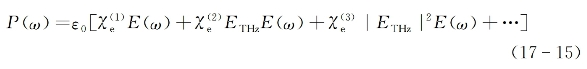
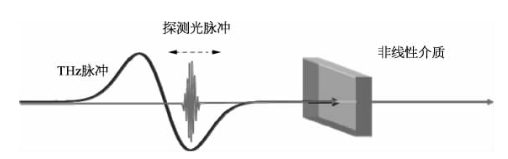
图17-9　一个单周期强太赫兹脉冲与一个弱超短探测光脉冲重合入射到一种二阶非线性介质的情况（前者在介质中产生的折射率变化，可导致后者经受相位调制与啁啾式频移，两入射脉冲之间的时间延迟可连续可调）

式中，是样品介质的第i阶有效非线性电极化系数。由探测光所感受到的折射率变化可写为

式中，是介质的线性折射率，而

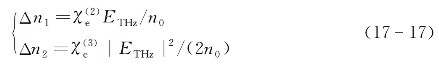
分别是由泡克耳斯效应和克尔效应引起的感应折射率变化。以常用的ZnTe晶体为例，=9.0×10-11 m/V，=3×10-19m2/V2［36］。相对于太赫兹场强ETHz=5×107 V/m，有Δn2/Δn1≈0.1；这说明在ETHz＜5×107 V/m条件下，泡克耳斯效应对ZnTe晶体内感应折射率变化的贡献是主要的。因此可将探测光脉冲经受的感应相位变化写为

式中，λ0是探测光在真空中的波长，L是ZnTe样品厚度，是表征泡克耳斯效应的有效二阶非线性极化系数，=1/υprobe-1/υTHz是行离参量并且其计算值为150 fs/mm，而υprobe与υTHz分别是探测光的群速度与THz脉冲的相速度。对探测光脉冲而言，它所经受的相位变化等价于晶体厚度随时间而变，则由于多普勒效应，探测光频率将发生如下的啁啾式变化：

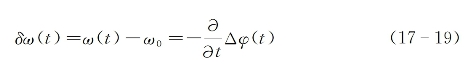
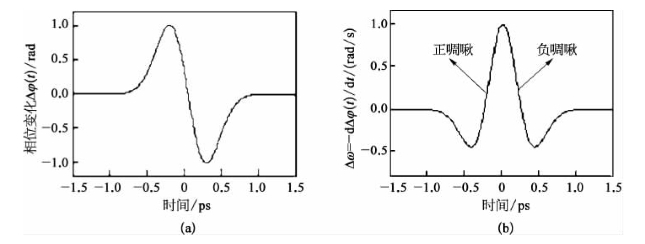
作为一个例子，图17-10（a）给出了在一种单周期太赫兹脉冲场入射作用下，按式（17-18）计算出的探测光感应相位的时间变化曲线；图17-10（b）为按式（17-19）计算出的探测光频移率随时间变化的啁啾曲线。通过比较这两条曲线发现，当通过改变相对时间延迟使窄探测光脉冲与太赫兹脉冲的不同时间段相互作用时，在太赫兹脉冲的前缘与后缘段，探测光脉冲将经历频率红移（δω＜0），在太赫兹脉冲两振幅峰之间的时段，探测光脉冲经历频率蓝移（δω＞0）；当探测光脉冲在时间上与太赫兹脉冲的中心段重合时，将经受最大的蓝移。这些理论预测特性，与下面描述的实验结果基本上是一致的。

(www.xing528.com)

图17-10　超短探测光脉冲经受的归一化相移（a）和归一化频移（b）（假设入射单周期太赫兹脉冲场波形如图17-9所示）［38］

以上所述这种利用强太赫兹脉冲场在介质中产生非线性光学效应的研究工作，已经由Shen等人所报道［37，38］。在他们的工作中，利用了基于电子加速器系统的相干太赫兹辐射源，输出单周期太赫兹脉冲能量为100μJ，持续时间为0.7 ps，对应的峰值电场强度为7×107 V/m。被研究的样品介质是ZnTe晶体，在输入太赫兹脉冲能量为35μJ水平时，在样品内产生的电场估算为4×107 V/m；在这样的电场水平下，对样品折射率变化的主要贡献来自泡克耳斯效应，而克尔效应的贡献可以忽略。用于检测这种折射率变化的探测光束出自钛宝石激光器，波长为795 nm而脉宽为120 fs。实验上，测量了探测光脉冲的光强（时空）分布以及相位和光谱随该脉冲与太赫兹脉冲之间的时间延迟而变化的动态行为。

图17-11给出了实验测量结果，从水平第1行所示结果来看，当不存在太赫兹场时，在探测脉冲整个持续时间内相位是恒定的，而光谱分布基本符合傅里叶变换极限。当探测光脉冲与太赫兹脉冲中心重合时，光谱出现最大蓝移，如图中第4行结果所示；当光脉冲与太赫兹脉冲的前缘和后缘重合时，其光谱表现为红移，如图中第2行和第6行结果所示。测得的探测光中心波长的最大蓝移为10 nm，最大红移为6 nm。

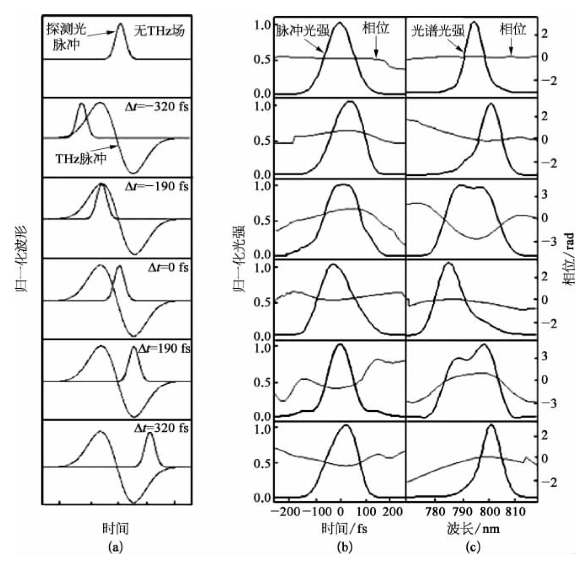
图17-11　单周期强太赫兹脉冲在ZnTe内通过泡克耳斯效应，对窄探测光脉冲产生互调制影响的实验结果［38］

（a）不同时间延迟时两脉冲的相对位置；（b），（c）不同时间延迟时测得探测光强与相位的时间与光谱分布

考虑到入射太赫兹波场不仅是时间的函数，也具有一定的横向空间分布，因此它不仅会导致探测光的相位调制，而且也会影响到探测光束的空间分布。假设一个半径为a的太赫兹脉冲波束在ZnTe晶体内传播，其横向场强近似为抛物线分布，则它在所经过的介质空间将引起如下的与横向坐标r有关的感应相位变化：

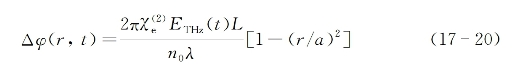
此时的非线性介质，等价于一个焦距为的透镜，这种感应透镜的焦距可通过改变太赫兹波场强而加以控制，例如当ETHz=4×107 V/m时焦距可短于35 cm。此情况下，如果让一个窄脉冲探测光束与太赫兹波束在空间重合传播，并调节时间延迟使得光脉冲与太赫兹正振幅峰位置重合，则有ETHz＞0和Δφ（r，t）＞0，因此探测光束将被聚焦；相反，如调节使光脉冲与太赫兹负振幅峰值重合，则有ETHz＜0和Δφ（r，t）＜0，探测光束将被散焦。这种决定于场振幅与相位的等价透镜，可称为感应“泡克耳斯透镜”，它区别于通常的只决定于光强的感应“克尔透镜”。

实验中，在探测光脉冲与太赫兹脉冲具有不同时间延迟条件下，测量了通过样品后，探测脉冲激光束横向光强分布对所施加太赫兹场强值的依赖关系。此情况下，探测光束本身通过光克尔效应引起的自聚焦影响可以忽略，实验结果如图17-12所示，图17-12（a）为太赫兹场不存在时透过光强空间的分布；图17-12（b），（c）为调节探测光脉冲与太赫兹脉冲不同场强值时段重合时测得的透过光强空间分布，显示出光斑尺寸随太赫兹场强增大而变小（自聚焦）；图17-12（d），（e）则表明当场强值进一步提高时，探测光束可发生分裂或具复杂分布；图17-12（f）显示，当探测光脉冲与太赫兹脉冲的负值时段重合时，探测光束光斑尺寸扩大（自散焦）。这些实验结果基本与以上的理论分析相符合。

图17-12　经过ZnTe晶体后透过探测光束的横向光强分布［38］

（a）不存在太赫兹场；（b）ETHz=2.5×107 V/m；（c）ETHz=4.0×107 V/m；
（d）ETHz=4.5×107 V/m；（e）ETHz=5.0×107 V/m；（f）ETHz=-4.0×107 V/m