慢光传输：基于电磁诱导透明非线性光学与光子学

在共振介质内实现慢光传输的原理与实现快光传输的原理正好相反。换句话说，为提供慢光传播，介质应该具有一个狭窄的增益线，或两个相邻窄吸收线，或在一个宽吸收背底下由饱和效应导致的窄吸收凹陷［见图16-8（b）］。

在慢光研究中，第一个突破是利用电磁诱导透明（EIT）原理，实现了在一种高度吸收介质中的慢光传播。EIT的基本概念和物理解释，曾由Harris等人给出十分清楚的阐述［28～30］。吸收介质的EIT机理，可参照图16-17（a）所示的三能级原子系统加以说明。其中原子大部分集聚于能级|1〉，而极少数集聚于能级|2〉。从|1〉至|3〉的频率为ω31和从|2〉至|3〉的频率为ω32的跃迁均是允许的。当一个频率为ω≈ω31的光单独入射时，介质将呈现出强的线性吸收。但是，如果有两个单色激光束同时作用于媒介，一个是频率为ωc≈ω32的强耦合光，而另一个是频率为ωp≈ω31的弱探测光，在这些特定的条件下，介质对探测光而言，可呈现为一种“透明”的媒介，这就是所谓的EIT效应，其实质是由于强耦合光促使粒子被相干地俘获在原子态|1〉，因此ωp≈ω31的跃迁实际上被禁戒［30］。

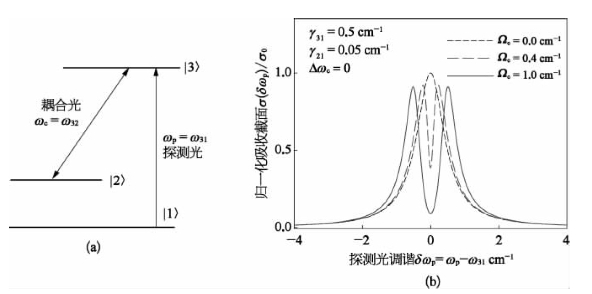
图16-17　吸收介质的电磁诱导透明（EIT）原理

（a）EIT原子系统的三能级结构；（b）归一化探测光吸收作为失共振量δωp=ωp-ω31的理论曲线［耦合光取3种不同拉比频率（Ωc）值，且有Δωc=ωc-ω32=0］

在这个特定的例子中，这两束光同时作用的结果，是使得整个原子系统被激励至由|1〉和|2〉组成的相干叠加态，而态|3〉始终保持是空的。换句话说，EIT可以解释为双光束与介质共振互动时产生的量子干涉效应。原子从态|1〉至态13〉跃迁的概率振幅，与从态|2〉至态|3〉跃迁的概率振幅基本相当，但两者的相位因子符号相反，故产生互为相消的量子干涉，从而使原子从|1〉至|3〉跃迁的净概率可以是零，其前提是耦合光束足够强而准确共振条件ωc≈ω32和ωp≈ω31得到满足。

基于EIT理论，假设Δωc=ωc-ω32=0，探测光的吸收截面可表示为失共振量δωp=ωp-ω31的函数［29］：

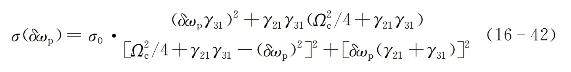
式中，σ0是当不施加耦合光束时|1〉→|3〉跃迁的峰值吸收截面，γ21和γ31是|1〉→|2〉跃迁和|1〉→|3〉跃迁的线宽因子，Ωc为耦合光束的拉比（Rabi）频率并定义为

式中，Ec为耦合光束的场强振幅，p0是原子|2〉→|3〉跃迁的偶极矩阵元。

图16-17（b）是针对3种不同Ωc值，由式（16-42）给出的探测光束吸收作为失共振调谐量δωp函数的归一化曲线。从该图可以看到，在耦合光场强取适当值时，可在探测光吸收曲线的中心频率附近，产生一个深而窄的吸收凹陷。在这种特殊情况下，由诱导透明导致在狭窄的频率范围内，可以出现折射率的陡变与提供巨大的正色散值，从而适用于慢光传播。

作为一个早期的理论估算，Harris等人专门考虑了一个10 cm长的208Pb（铅）原子蒸气系统，原子密度假设为7×1015/cm3［31］。以波长为405.9 nm以及拉比频率为Ωc≈0.7 cm-1的耦合光束激励原子的6s2 6p23P2→6s2 6p7s 3P1跃迁，再同时以波长为283 nm的弱探测光来激励6s2 6p23P0→6s2 6p7s 3P1跃迁，在这种情况下，计算出探测光脉冲的群速度为υg≈c/250。1995年，Kasapi等人完成了在以前提出的208 Pb原子蒸气系统中的实验研究，他们使用波长为406 nm而持续时间为100 ns的激光脉冲作为耦合光束，并采用波长为283 nm、持续时间为12 ns的激光脉冲为探测光束［32］，在蒸气样品长度为10 cm、原子密度N0≈2×1014/cm3、283 nm波长处普通线性吸收系数为α0=600 cm-1的实验条件下，所测得的使用和不使用耦合光束两种情况下，探测脉冲光的透过曲线如图16-18所示。基于脉冲延迟测量的结果，探测光脉冲的群速度值为υg=c/165，而透过率值为55%。(www.xing528.com)

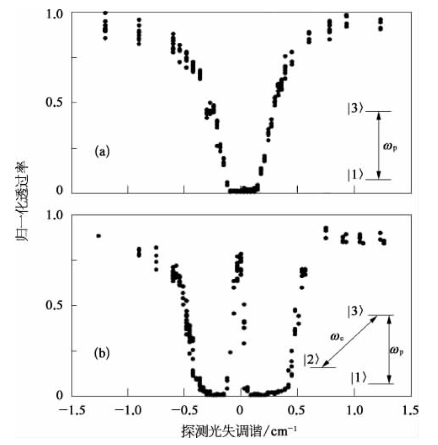
图16-18　在208 Pb蒸气系统中测量的透过探测光脉冲作为失共振调谐的函数曲线［32］

（a）探测光单独入射；（b）探测光与拉比频率为Ωc=0.4 cm-1的耦合光同时入射

与此同时，Xiao等人也报道了使用工作在20℃的76 mm长的Rb（铷）蒸气样品，使得EIT发生在一种级联三能级系统。他们在探测光透过率曲线的中心频率处，测得最大的正色散量为1.94×10-8 s，这对应于一个υg=c/13.2的群速度［33］。

Hau等人于1999年报道了一个具有极低群速度υg=17 m/s的实验结果，它是在采用激光方法冷却到nK（纳开氏温度）的超冷Na（钠）原子云体系中实现的［34］。样品的厚度与原子密度分别为L=229 μm和N0≈5×1012 cm-3，而系统则处于玻色爱因斯坦凝聚状态。波长为589 nm的弱探测激光与原子的D2线共振，并对应于从基态32S1/2的|1〉=|F=1，MF=-1〉超精细能级至较高能态32 P3/2的|3〉=|F=2，MF=-2〉能级的跃迁，强耦合激光则调谐到与从基态中另一超精细能级|2〉=|F=2，MF=-2〉至同一高能级的跃迁产生共振。图16-19（a）给出了钠原子的部分能级图，并分别给出了耦合和探测光的跃迁途径。

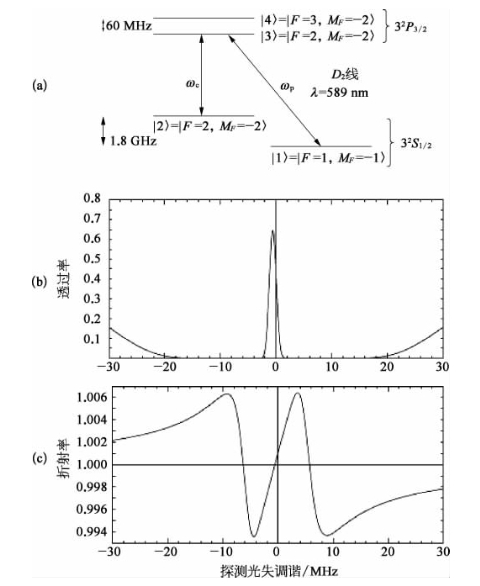
图16-19　钠原子的部分能级图和为实现EIT而采用的耦合光及探测光跃迁（a）、探测光透过率作为失共振调谐函数的计算曲线（b）、对探测光而言的折射率色散计算曲线（c）（在零点处透射峰值的移位是因耦合光场对|2〉能级的斯塔克效应所导致）［34］

图16-19（b）和（c）给出了对探测光而言的透过率和折射率作为共振失调谐函数的计算曲线，条件是温度T=450 nK，N0=3.3×1012 cm-3，厚度L=229 μm，耦合光强Ic=52mW/cm2。由于该超冷介质的|1〉→|2〉跃迁具非常小的多普勒展宽，即使在较低的耦合光强度下，亦可对探测光脉冲呈现出在远小于|1〉→|3〉跃迁自然宽度内的诱导透明高峰，并从而导致一个非常陡峭的折射率正色散突变。

图16-20为实验测得的透过探测脉冲相对于参考脉冲的时间延迟为Δt=7.05 s，对应的群速度值为υg=32.5 m/s。在最佳条件下，测量到的最低群速度是17 m/s。

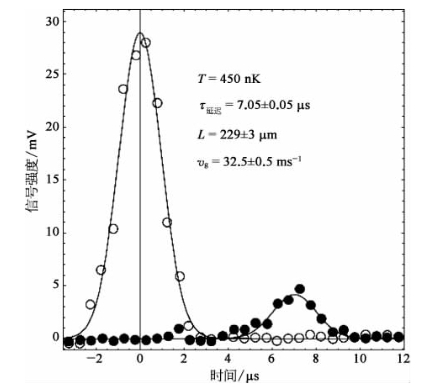
图16-20　测量到的探测光脉冲的时间延迟，对应于υg=32.5±0.5 m/s的群速度（空心圆圈表示无原子云时记录到的参考脉冲，实心圆点表示有原子云时记录到的透过探测脉冲，实线表示用高斯线型拟合的曲线）［34］

基于相同的EIT机制，Kash等人报道了他们在2.5 cm长，温度为360 K并加入缓冲氖气的87 Rb原子蒸气系统中，测量到探测光脉冲延迟量为Δt=0.26 ms，相应的群速度值为υg=90m/s［35］。此外，Budker等人也报道了基于相似的EIT机制，在85 Rb蒸气系统中，测量到更慢的群速度值υg=8m/s［36］。