复折射率:吸收介质的研究结果

如5.1节所述，一个各向同性的线性吸收介质的线性电极化率在共振吸收区附近是一个复数量，与此相应，亦可在此引入一个广义的介质线性折射率，它可以表示为以下的复数形式：

式中，n与n'分别是的实部与虚部。而此时的线性电极化率χ（1）（ω）可表示为

式中，为非共振贡献（实数），为共振贡献（复数），且它包含了实部和虚部。从式（5-8）可知，

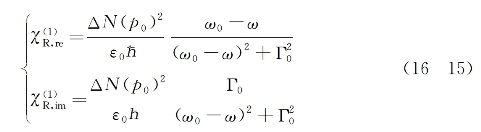
式中，ΔN为所考虑的吸收介质低-高两能级间的粒子数之差，p0是介质分子电偶极矩矩阵元，ω0为吸收跃迁中心频率，而2Γ0是吸收跃迁谱线的全宽。将式（16-14）代入式（16-13）可得

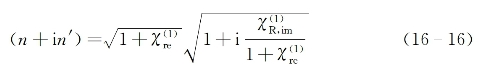
式中，为χ（1）的实部。因为和两者在量值上相近并且都显著小于，故有

令等式（16-17）两端的实部和虚部分别相等后可求实折射率为

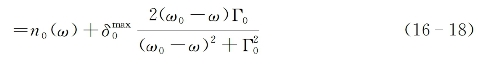
式中，为出自非共振贡献的折射率值，是折射率的共振贡献相对于非共振贡献的差异极大值，并可写为

从式（16-17）出发亦可得出复数折射率的虚部为

式中假设了显著小于非共振折射率n0。将式（16-15）中第二式代入式（16-20）后可得(https://www.xing528.com)

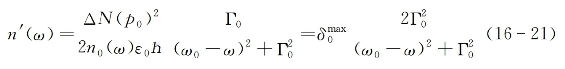
另一方面，一种在吸收介质中沿z方向行进的单色平面波为

式中，为广义波矢量的绝对值，它由复折射率所决定：

式中，λ0为与ω0对应的真空中的波长。将式（16-23）代入式（16-22）可得

经过z距离后光强的衰减为

式中，α（ω）为介质的线性吸收系数并决定于复数折射率的虚部：

将式（16-21）代入式（16-26）可得α（ω）的最终表达式为

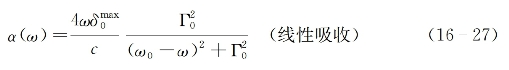
比较式（16-27）与式（16-18），可以看出在吸收介质中线性吸收系数α（ω）和（线性）折射率n（ω）两者均由关键参量的大小所决定。作为一个定量的例子，图16-2（a）与（b）分别为α（ω）与n（ω）作为变量（ω-ω0）/Γ0的函数曲线，此处假设=0.15，n0=1.2，ω0=2π×5×1014 s-1，ω0/Γ0=200。

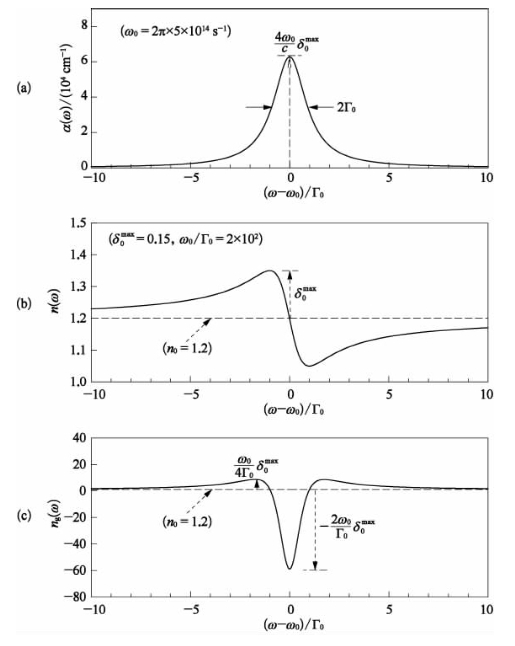
图16-2　吸收介质的线性吸收曲线（a）、折射率色散曲线（b）、群折射率曲线（c）

图16-2（a）表明了线性吸收系数α（ω）在ω=ω0位置处达到其极大值；而图16-2（b）则表明折射率n（ω）在|ω-ω0|=Γ0位置处与n0值的最大偏离。