超短激光脉冲的自相关测量-非线性光学与光子学

通常用于测量超短激光脉冲时间宽度的常规方法，是基于自相关或互相关二次谐波的产生。在这种情况下，二阶非线性晶体的相位匹配要求必须满足，而作为两入射基频脉冲相对延迟时间函数的二次谐波信号，通常是由光电倍增管加以检测。这样探测到的信号强度可以表示为

式中，与是两个基频脉冲光强的时间函数，Δt是这两个脉冲之间的时间延迟。如果假设基频光脉冲的波形形状已知并且在时间尺度上是对称的，则其真正的脉冲宽度很容易由相应的I2v（Δt）测量曲线的宽度所决定。然而，如果输入基频脉冲形状在时间尺度上不对称，则这样一种不对称是不能使用这种二阶强度相关的方法而检测到的。

以下要介绍的方法，是基于发生在半导体光电探测器内的双光子或三光子诱导光电导效应，它可用来测量超短激光脉冲的时间波形，此时不存在任何相位匹配要求。例如，在采用二阶自相关激励机制时，可将待测超短脉冲的激光分成两束并予以相对时间延迟，然后使这两束脉冲激光空间重合地聚焦入射到选定的半导体探测器。在双光子激发情况下，这样记录到的光电流（或电压）的变化，可表示为如下相对延迟时间的函数：

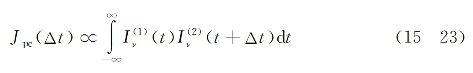
同样的原理也适用于频率非简并二阶互相关的情况，亦即两入射脉冲激光可以具有不同的频率。

实验中，已经采用多种商品半导体光电二极管作为双光子或三光子诱导光电导自相关器来测量激光脉冲宽度，其中包括Si［71］，GaAsP［71，72］，SiC［73］，GaN［74］，SiC［75］，AlGaAs［76］以及金刚石二极管等［77］。同样，也曾利用另外一些具有片状或波导状的半导体光电元件（如CdS［71］，ZnSe［78］，GaAs［79，80］以及GaN等［81］）进行激光脉冲的自相关测量。此外，利用能带间隙为Eg≈9 eV并施以偏压的熔融石英样品，也实现了对波长为267 nm的紫外超短激光脉冲的自相关测量［82］。

先来考查一个由Schade等人报道的基于双光子光电导的互相关实验，探测元件为GaAsP扩散二极管，能带间隙为Eg≈1.8 eV［83］。一束输入脉冲激光的波长为λ1=775 nm，另一束输入脉冲激光的波长为λ2=1 300 nm，所测得的由非简并双光子吸收导致的光电流信号随两入射脉冲时间延迟变化的数据如图15-12（a）所示，这些数据可以很好地用一个时宽为299 fs的高斯函数予以拟合。除此之外，在λ1=775 nm的输入光束功率固定在28 mW的条件下，测得最大光电流随λ2=1 300 nm输入光束功率而变化的数据如图15-12（b）所示，显示出一种线性的关系。这后一结果是可以理解的，因为最大相关光电流信号应正比于两个光束功率的乘积。

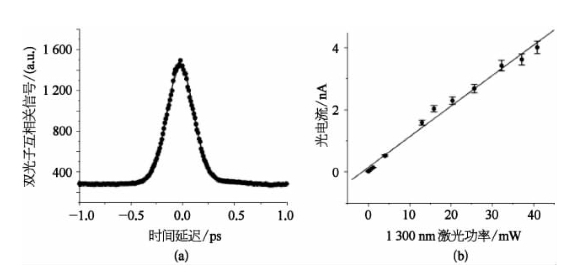
图15-12　采用GaAsP光电二极管测量非简并双光子光电导互相关信号的实验数据以及用时宽为259 fs高斯函数拟合的曲线（a），在λ1=775 nm输入光束功率固定为28 mW条件下，测得的光电导信号对λ2=1 300 nm光束功率的依赖关系（b）［83］

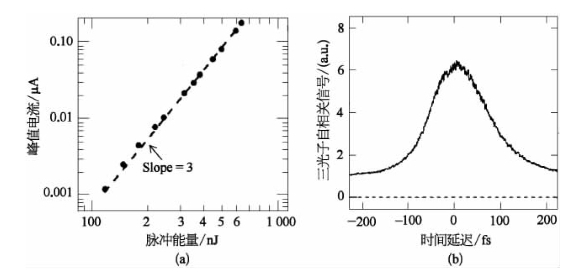
下一个实例考虑一个由Streltsov等人完成的基于三光子诱导光电导的自相关实验，其中采用了带隙为Eg≈3.4 eV的GaN（氮化镓）光电二极管，以脉宽为60 fs、波长为820 nm（1.51 eV）的激光进行辐照［74］。图15-13（a）给出了峰值光电流数据作为输入脉冲能量的函数，表明了三光子激发过程的立方依赖特征。而图15-13（b）则给出了在两入射光束光强略有不同条件下，测得的三阶光强自相关信号强度作为两光束相对时间延迟的变化曲线，这里应注意到，不相等的两束光强导致了自相关曲线形状的轻微不对称。

(www.xing528.com)

图15-13　在GaN光电二极管中产生的三光子诱导光电流峰值随输入激光脉冲能量的变化曲线（a）以及在两入射光束的光强略有不同条件下测得的自相关扫描曲线（b）［74］

为解释在三阶光强相关实验中，使用光强不等的两束光入射或者形状不对称的光脉冲入射，可以破除为二阶光强相关实验所固有而无法检测脉冲形状是否对称的局限性，可以把三光子诱导光电流表示为两入射脉冲时间延迟（Δt）的函数：

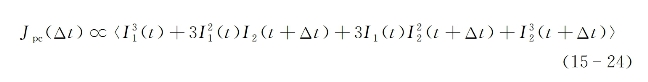
式中，I1与I2为两脉冲光束的光强，符号〈〉表示对时间求平均。进一步假设a=I1/I2＜＜1，上式可改写为

如果a＜＜1，上式中第一项和第二项可忽略，从而最后有［84］

在式（15-25）右端，第二项仅给出直流背底贡献，而第一项则决定了三阶光强自相关曲线，后者可反映出入射激光脉冲形状的不对称性。

为证实三阶强度相关的上述特性，Langlois与Ippen完成了一个实验：采用GaAsP光电二极管作为三阶自相关器、硅光电二极管作为二阶自相关器，两者都使用1.5μm的双脉冲激光进行激励［84］。实验中，作为时间形状不对称的入射双脉冲激光信号，是由两个持续时间各为138 fs而间隔为320 fs的子脉冲组成的，两子脉冲的峰值强度比为14。这样一种双脉冲激光经分束后，以相对延迟的两光束方式空间重合入射到上述两自相关器之一，而两光束的光强比选择为a=0.04。按这种方式测得的二阶和三阶自相关曲线如图15-14所示，可见，只有后者才能揭示出输入脉冲信号的不对称（双峰）结构。

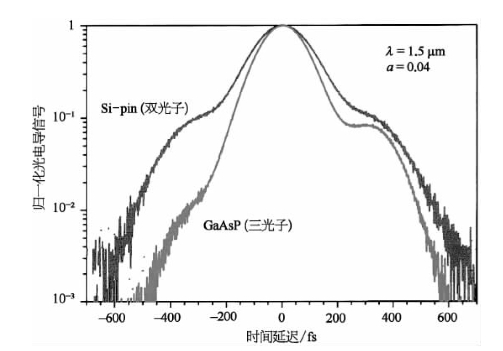
图15-14　利用具不对称双脉冲结构的1.5 μm激光产生的二阶（双光子）与三阶（三光子）自相关实验曲线［84］