光子吸收的定量表述：辐射量子理论研究成果

1）双光子吸收过程

采用辐射的量子理论方法，并经由与分子拉曼散射微分截面基本相同的推导过程（参见7.2.2节），可同样得出表征单个分子同时吸收两个入射光子能力大小的微分吸收截面。上述两种过程的唯一区别是，对单个分子的拉曼散射来说，第一步是分子由起始能级通过一个入射光子的湮灭而跃迁至中间能态，第二步是分子通过一个散射光子的产生而由中间能态跃迁至拉曼（通常为振动）激发态；而对双光子吸收过程来说，第一步是分子吸收一个入射光子而跃迁至中间能态，第二步则是该分子通过吸收另外一个入射光子而由中间能态再跃迁至更高的一个电子激发态。在后一种情况下，假设有两种不同频率（v1和v2）的两线偏振入射激光束同时重合入射到一给定的双光子吸收介质，并且两束入射光的截面（S）和发散角（Ω0）相同，则与式（7-42）相似，可以直接写出单个分子在单位时间内从两入射光束中同时各吸收一个光子的概率为

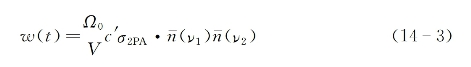
式中，V是两入射光束在介质内的重合作用空间体积，c'是介质中光速，和分别为两入射光束的光子简并度，而σ2PA则是分子的双光子吸收微分截面（单位是cm2），它可参照式（7-45）给出为

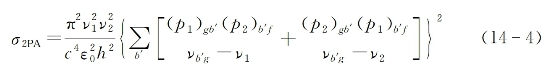
式中，c为真空中光速，ε0为真空中介电常数，h为普朗克常数，p1和p2是分子电偶极矩矢量算符分别在两入射光偏振方向上的投影分量，它们的跃迁矩阵元的角标g和f分别代表分子双光子吸收跃迁的初始和终止本征能级，而式中的求和则是按分子的所有本征激发态b'（f态除外）进行。以上是假设两入射光均为线偏振前提下导出的公式，对于两种入射光频率具有更复杂偏振状态的情况，也可导出基本相似的双光子吸收截面表示式［10］。

如果进一步假设无入射光作用时分子全部处于基能态g，在该能态上的分子数密度（单位是cm-3）为Ng=N0，这里N0是散射介质的分子密度，而分子能产生双光子跃迁的始终能级间隔为hvfg，则在两束入射光频率满足如下共振要求的前提下：

按照式（14-3），N0V个分子在单位时间内的双光子吸收总概率应为

基于上面导出的式（14-6），可将单位时间内入射光束1光子简并度的减少表示为

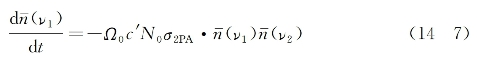
再利用光子简并度与光束功率（P）或光强（I）的关系式［参见式（1-24）］：

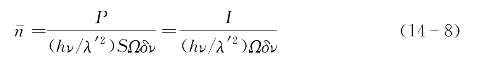
式中，λ'为光在介质中的波长，而式（14-7）可改写为

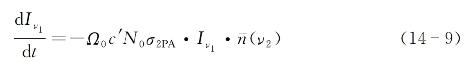
式中，Iv1为光束1的光强。

在稳态近似下，在介质内有dt=dz/c'，则由式（14-9）可得

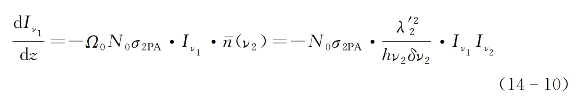
式中，为第2束入射光在介质中的波长，δv2为第2束入射光束的光谱宽度。上式的物理意义是其中一束光的光强衰减与两束光的光强乘积成正比。考虑到2PA与线性吸收相比是一微弱的非线性过程，即使在远大于波长的传播距离上第2束光强的衰减变化也很小，则可认为在上式中Iv。近似为常数，因此有

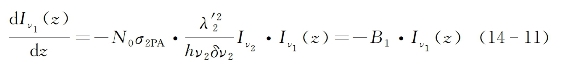
其解为

式中，系数B1（单位是cm-1）为

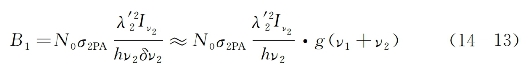(www.xing528.com)

式（14-13）中的g（v1+v2）是一个双光子吸收谱线形状函数，具有与1/δv2相同的量纲。在B1z＜＜1的情况下，近似有

对光束2同样可推导出完全相似的表示式。

本节按辐射量子理论导出的分子2PA微分截面表示式（14-4）以及2PA引起的光束按传播方向的衰减公式（14-12），与9.3.2节中按半经典理论导出的相应公式（9-43）以及式（9-44）基本相同。

在只有一束频率为v的线偏振激光入射并满足2v=vfg的条件下，分子的2PA微分截面参照式（14-4）可表示为

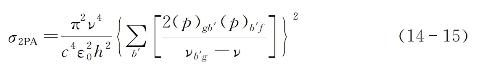
式中，（p）gb'等为分子偶极矩矢量算符在入射光偏振方向投影分量的相应跃迁矩阵元。而由2PA导致的该光束光强的衰减，可按式（14-10）直接写为

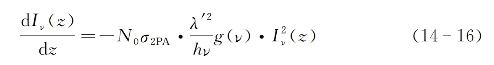
式中，g（v）是一个给定介质的双光子吸收谱线形状因子。

2）三光子吸收过程

一般情况下的三光子吸收过程可由图14-1（b）加以描述，此时假设有3种频率不同的光束同时重合入射到一给定非线性吸收介质，组成该介质的一个分子可借助同时表征该分子与入射光子场的两个中间能级（虚能级），通过吸收3个频率不同的入射光子而完成从其基态至某一高电子激发态的跃迁。这样一种过程的有效产生，必须满足能量守恒条件：

基于与双光子吸收过程基本相同的全量子理论推导方法，可以求出分子的多光子（≥3）吸收微分截面以及其中任意一个入射光束的光强衰减公式［1］。为简明起见，这里只考虑频率简并三光子吸收过程，亦即只有一种频率为v的强光束入射的情况，此时要求能量守恒条件3hv=hvfg得到满足，而表征单个分子的三光子吸收微分截面（量纲为cm2）可求出为［1］

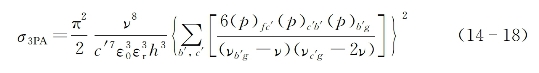
式中，c'为入射光在介质中的速度，εr为介质在入射光频率处的相对介电常数，p为分子电偶极矩矢量算符在入射光偏振方向上的投影，角标b'与c'分别代表分子本身的所有可能的本征能级（初始态g与终态f除外）。

设频率为v的线偏振单束强入射光束的立体发散角为Ω0，频宽为δv，光子简并度为，别单位时间内由于三光子吸收导致的入射光子简并度的减少可求出为［1］

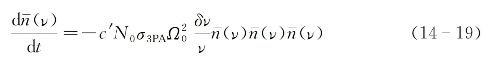
式中，N0为具非线性吸收能力的分子密度。进一步利用光子简并度与入射光强的关系式（14-8），则入射光强随时间的变化可表示为

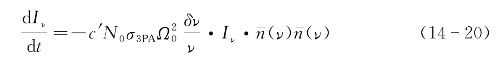
此种情况下，可将I（v'）随时间的变化理解为沿光行进方向（z轴）上的衰减变化。为此，可在式（14-20）中令dt=dz/c'而得

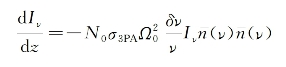
式（14-21）的物理意义是，由三光子吸收导致的光强在其传播途径上某处的衰减率，是正比于该处光强的三次方。这一结论，可以推广到更多（m＞3）光子同时吸收的过程，此情况下入射光强在行进方向某处的衰减，正比于该处局部光强的m次方。