空间亮孤子在二阶非线性介质中的形成

如前所述，在透明光学晶体中，与非共振的三次非线性光学效应相比，二阶非线性光学效应是非常容易被观察到的。在这类不具中心对称的二阶非线性晶体介质中，通常所称的三波混频（包括二次谐波和光学参量过程），不仅能导致参与作用的不同频率组分之间的能量耦合交换，而且也能导致在不同组分频率处的感应折射率变化，从而也可以导致自聚焦效应［19，20］。据此，人们可以期望，空间亮孤子亦可在二阶非线性介质中产生和被观测到［21，22］。此情况下，介质折射率的感应变化是源自电子云畸变，因此具有瞬时反应的特点。

与三阶非线性过程导致的折射率变化相对于入射光场的依赖性有所不同，在二阶非线性介质中，由三波混频过程导致的折射率变化，在量纲上不是正比于光强，而是正比于光场的振幅。以二次谐波混频过程为例，假设频率为ω的基频光束和频率为2ω的倍频光束，同时亦满足相位匹配（类型Ⅰ）的方式入射到某一倍频晶体中，根据第5章给出的理论分析［参见式（5-64）］，在两种作用光束频率处的感应折射率变化为［20］

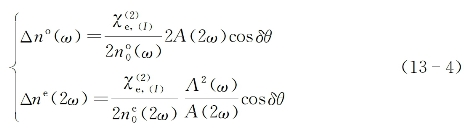
式中，Δno（ω）和Δne（2ω）分别表示基频（o寻常光）和倍频（e非寻常光）处的折射率变化量，A（ω）和A（2ω）分别是两光束的振幅，是满足类型Ⅰ相位匹配条件下晶体的有效二阶非线性电极化系数，而δθ是两作用光束间的相位差。从上式可以看出，当δθ=0或2mπ（m为一整数）时，介质相对于两作用光束均产生最大的正折射率变化（有利于自聚焦）；当δθ=m'π（m'为一奇数）时，介质对两光束产生最大的负折射率变化（有利于自散焦）；最后当δθ=m'π/2时，对两作用光束而言不产生折射率的感应变化，但此时却可在两光束间产生最有效的能量交换。式（13-4）的物理含义是，两作用光束之间可同时产生互自聚焦或互自散焦，视它们之间入射时的初始相位差而定。对满足类型Ⅱ相位匹配条件入射而言，可导出与式（13-4）相类似的折射率变化表达式。同样的物理考虑，也可推广到其他的三波混频过程，包括和频过程和频率下转换参量过程。

在二次非线性介质内产生二维空间亮孤子的首次实验报道，由Torruellas等人发表于1995年［23］。该实验中，非线性介质为1 cm长的KTP晶体，一个很强的1 064 nm基频光束和一个很弱的532 nm的倍频光束以满足类型Ⅱ匹配方式同时重合入射到晶体样品中。两光束的脉冲宽度均约为15 ps，其中532 nm光束在入射前先通过一个30 cm长而充气压可变的气体盒，通过改变气体盒中的充气压，可控制和改变两入射光束间的相位差。经过透镜聚焦后的强基频光束在晶体入射端面处的光斑尺寸约为20 μm，而与其对应的瑞利范围约为2 mm。在没有倍频光入射或者基频光入射光强很低的情况下，样品出射端面处基频光的光斑尺寸增加到≥80 μm，如图13-2（a）所示。当倍频光同时并且同相位入射，而基频光强为5～10 GW/cm2的条件下，在样品出射端面处的1 064 nm光束的光斑尺寸可被压缩到12.5 μm，如图13-2（b）所示，这可看作是空间亮孤子形成的标志。在同样的入射光强条件下，若两束光的入射相位差被变动180°，则光学自陷效应消失，如图13-2（c）所示。稍后，在基本相同的实验条件下，以一很强的532 nm光束和一很弱的1 064 nm光束同时同相位入射，观察到两光束同时形成的空间光学孤子［24］。(www.xing528.com)

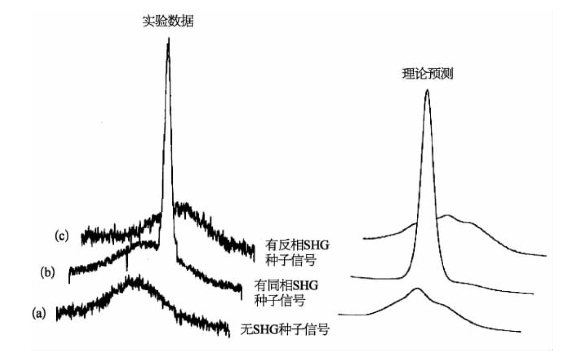
图13-2　输出基波光束剖面横向光强分布［23］

（a）无二次谐波（SHG）光输入；（b）有同相二次谐波光输入；（c）有反相（180°）二次谐波光输入

进一步研究表明，在相位匹配条件近似得到满足的条件下，即或采用一个聚焦的强基频光束单独入射到倍频晶体样品中，通过该光束与其在晶体中新产生的倍频光束之间的相互作用，亦可通过对两光束在样品输出端的光斑尺寸的测量，证实两光束在晶体内传播过程中空间亮孤子的形成［25，26］。在此情形下，两光束之间的能量交换和彼此导致的折射率变化可在晶体内同时产生。类似的多光束空间光学孤子的产生，亦在二次非线性晶体中，通过实现频率下转换（ωpωs+ωi）参量过程而成功观测到［27，28］。