拉曼增益导致的时间孤子的自频移效应

12.2.5节已经讨论了利用外部泵浦产生的拉曼增益来补偿光纤损耗，从而确保时间孤子在光纤中的远距离传输的课题。在那种情况下，即使提供很低（0.2 dB/km）的拉曼增益已经足够克服光纤的损耗影响；在这样低的增益水平下，如果没有信号光束的输入，光纤本身是不足以产生受激拉曼散射信号的。现在考虑另外一种情况，即在无外加拉曼泵浦光的前提下，考虑到石英玻璃材料的拉曼增益曲线在频移值很小［例如20～50 cm-1］时仍然不趋近于零，因此在入射光脉冲具有较宽频谱的条件下，可把较高频率的光谱组分想象为泵浦光，而较低频率的组分作为信号光，则在光纤传输过程中，脉冲中高频组分的能量将经由拉曼增益机制向低频组分转移。这种过程持续进行的结果，最终导致输出光脉冲的频谱出现向低频方向的持续移动和相应的加宽。

这种效应，Dianov等于1985年曾由实验观察到，他们当时以250 m长的单模光纤做样品，使用了波长为1.54 μm、时间宽度为30 ps的光脉冲入射并产生高阶时间孤子［25］。入射脉冲的峰值可在50～900 W范围内变化，而在100 W的水平下对应的孤子阶数为N≈30。图12-9为在不同输入峰值水平下，测得的输出脉冲的光谱分布曲线［（a）～（d）］，从中可以看出在高功率输入水平下，光谱逐渐加宽，并且能量优先向低频方向转移。在中等输入功率下观察到的对称型加宽，可通过与自相位调制同时发生的光谱自加宽效应加以解释；而在高功率输入条件下出现的光谱非对称加宽，则可由上述的自泵浦拉曼增益效应予以理解。图12-9（e），（f）则分别表示在初始入射脉冲的中心波长（1.54 μm）处以及红移后的1.55 μm波长处测得的自相关描述曲线，可明显看出红移加宽后的光谱组分所对应的脉冲持续时间明显变短。

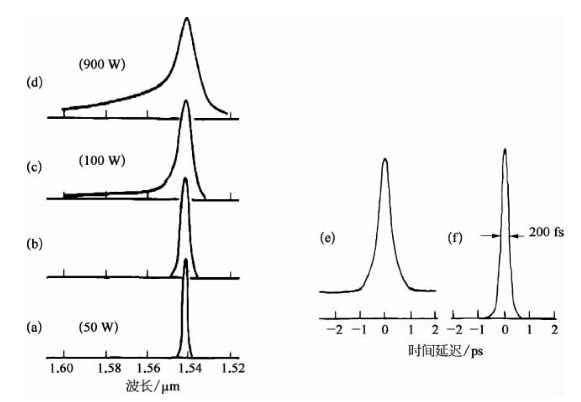
图12-9　不同输入功率水平下，波长为1.54 μm、时间宽度为30 ps的光脉冲经过250 m长光纤样品后测得的光谱分布曲线［（a）～（d）］以及在1.54 μm和1.55 μm波长位置处测得的输出脉冲自相关曲线（输入脉冲功率为900 W）［（e），（f）］［25］

相类似的实验结果也被Mitshke与Mollenauer观察到［26］。在他们的实验中，使用了持续时间更短（0.5 ps）的入射脉冲，其峰值功率约几倍高于计算所得的P1大小，而所用光纤的长度可在50～392 m间变动。实验发现，经过光纤样品后的出射脉冲可含有时间前后分开的组分，光谱的红移随样品长度以及输入功率的增加而变大，其频移范围可达100 cm-1以上。这些事实证实了级联拉曼能量转移的机制，也与理论分析的结果基本相符［27，28］。(www.xing528.com)

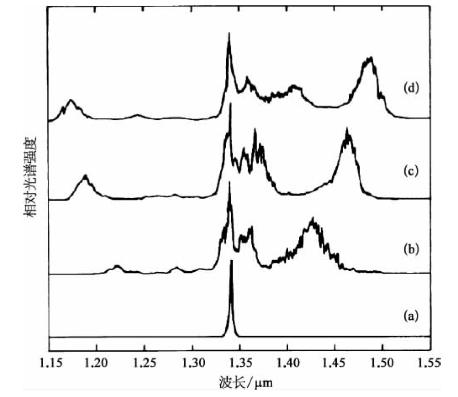
图12-10　时间孤子在光纤中引起的频率加宽和自移动［29］

（a）1.341 μm输入脉冲的光谱；（b）～（d）经过光纤长度分别为17，50，150 m后的输出脉冲光谱（输入脉冲时间宽度为0.83 ps，峰值功率为531W）

然而，在其他一些条件下所做的实验表明，由时间孤子入射在光纤中引起的频率加宽和自移动，亦可在入射脉冲中心波长的两侧同时观察到［29，30］。作为这类实验观察的一个例子，图12-10为采用波长为1.341 μm、宽度为0.83 ps的光脉冲，入射到不同长度的光纤样品后测得的输出脉冲光谱曲线［29］。输入脉冲的峰值功率为531 W，光纤样品的零GVD波长位置处于1.317 μm，而其长度则可在17～150 m范围内改变。由图12-10可见，经过光纤样品后出射光脉冲包括的附加光谱组分，可在入射光脉冲中心波长的高、低频两侧同时观察到。这些附加组分相对于原中心波长位置的频移，与光纤样品长度成正比的关系；而低频移的光谱组分的能量总是远大于高频移组分。以上所述三个事实中的第一个，可由拉曼增强的四波混频（四光子参量作用）机制加以解释［30］；第二个事实，表明了产生四光子参量作用的种子信号是由与自调制效应相关联的光谱自加宽过程所提供，这后一过程随光纤长度的增加而增强；第三个事实，则可由高频移组分的反拉曼（衰减）作用加以解释。