实验证明：光纤中时间孤子效应的发现

最早在光纤中证实光学时间孤子存在的实验结果由Mollenauer与Gordon在1980年发表［5］。在该实验中，入射光波长约为1.55 μm，脉冲宽度约为7 ps，近似具有sech2的形状，重复率为100 MHz。所用的是700 m长的单模石英玻璃光纤，芯径为9.3μm，在1.55 μm波长处的GVD系数为D≈-16 ps/（nm·km）。在上述条件下，根据式（12-18）计算出的孤子周期为z0≈1 260 m，而为形成基本孤子所要求的脉冲峰值功率约为P1=1 W。实验中用改变入射脉冲峰值功率的方法，来考查在适当入射功率水平下相应阶次的时间孤子的形成规律。由于光纤样品的长度（L=700 m）近似等于孤子周期值z0的一半，因此由图12-3所示的各阶孤子在z0/2距离处的理论行为，可直接用来与实验观察相比照。

图12-4为不同入射脉冲峰值功率水平下，测得的光纤样品输出脉冲的二次谐波自相关曲线以及相应的输出脉冲的频谱曲线。由图可知，当入射脉冲功率P＜＜P1时，输出脉冲的宽度略大于入射脉冲宽度，这是由于群速度色散效应所导致。当P≈P1或N≈1时，输出脉冲宽度与输入脉冲基本相同，这意味着在任何传输距离上，上述脉冲加宽都正好被自调制效应所补偿。当P≈4P1时，输出脉冲明显变窄，这表明N=2孤子的形成。当P≈9P1时，N=3孤子开始形成，其标志是输出脉冲的自相关扫描曲线有三个峰值（对应两个脉冲峰值），正如图12-3中理论所预计的那样。

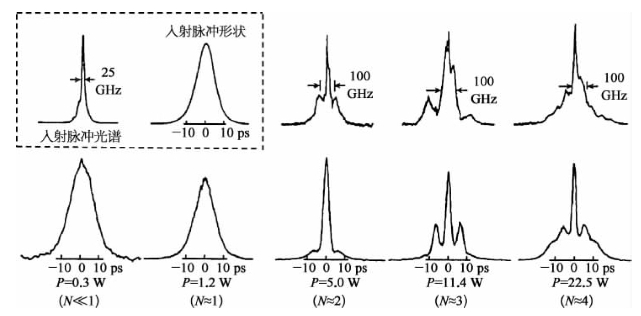
图12-4　输出脉冲自相关二次谐波信号扫描记录（下）以及相应的频谱描述曲线（上）（方框中所示为入射光脉冲的相应测量结果，光纤样品长度L≈z0/2）［5］(www.xing528.com)

实测到的入射光脉冲频谱和输出光脉冲的频谱曲线如图12-4顶部方框内所示。从中可以对照看出，当出射脉冲时间宽度变窄时，其对应的频谱宽度同时变宽；这是由测不准关系或数学上的傅里叶变换关系所决定的。至于较高阶时间孤子在传输过程中时间波形与频谱行为的复杂变化行为，均可以从GVD效应与自相位调制效应之间的动态相互作用和影响而加以解释。

对于入射初始光脉冲不满足A=N［见式（12-15）］的情况，其在光纤中的传输行为在理论上亦有所分析［4，6］，在实验上也曾有所研究［7］。