式(12-14)可以完美地用来描述工作在负GVD区域内单模石英玻璃光纤中时间孤子的形成[5]。为此,首先假设入射光脉冲具有振幅包络线形式:
![]()
式中A为无量纲的振幅极大值,而s0=t/τ0。当t=τ0时,sech(s0=1)=0.648;这意味着此情况下r0可粗略地用来表征入射光脉冲振幅包络线波形的半宽度。在数学上已经证明,式(12-14)的孤子解在介质入射面应满足条件:
![]()
式中,N可为任意正整数。对于N=1以及N=2,时间孤子解具有如下的解析表达式[4]:

通常称N=1对应的孤子解为基本孤子解,它的包络线形状和宽度在非线性介质传输过程中始终保持不变。而对于(N=2,3,4…)等高阶孤子而言,它们的包络线函数的形状和宽度,则沿介质传输距离上呈现周期性的变化,其变化的距离周期相同,并等于ξ0=π/2。在实验室坐标内,这一周期为

式中,D(λ)为单模光纤在脉冲中心波长λ0处的GVD系数。对高阶孤子而言,它们初始的包络线形状和宽度,在经过每一传输周期z0后保持重复再现。(https://www.xing528.com)
对于N=1的基本时间孤子来说,由式(12-16)可知umax=1,则由式(12-13)可求出为形成基本孤子而要求的入射光脉冲的峰值功率为
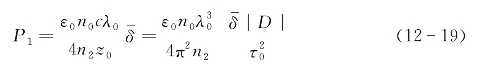
式中,![]() 为光纤的横截面。上式的物理含义是:为形成基本时间孤子所要求的入射脉冲峰值功率正比于光纤的GVD系数(|D|),而反比于
为光纤的横截面。上式的物理含义是:为形成基本时间孤子所要求的入射脉冲峰值功率正比于光纤的GVD系数(|D|),而反比于![]() 。这里应该指出的是,为形成第N阶孤子与形成基本孤子所需要的峰值功率之比为PN/P1=N2。
。这里应该指出的是,为形成第N阶孤子与形成基本孤子所需要的峰值功率之比为PN/P1=N2。
图12-3给出了N=1,2,3三种时间孤子沿单模光纤传输距离上的功率包络线波形的理论变化行为[5]。由该图可以看出,基本孤子的时间波型在整个传输过程中保持不变。对于N=2的光学孤子,它在z0/2距离处脉冲变窄和峰值变高。对N=3的光学孤子,它在z0/4以及3z0/4位置处脉冲更加显著变宽,而在z0/2位置处脉冲分裂为二。对于N=4的孤子来说(未在图中显示),它在z0/2位置处分裂为三。

图12-3 基本(N=1)时间孤子以及两个(N=2,3)高阶孤子沿光纤内传输距离z上的功率包络线形状的理论变化行为(z0为孤子变化周期)[5]
为了利用式(12-18)与式(12-19)更准确地计算z0和P1的数值,可对式中所含关键的时间因子τ0进行更严密的确定。如果假设实际入射光脉冲具有sech2形式的功率包络线,其半峰全宽(FWHM)为τ,而与其对应的sech形式的振幅包络线的FWHM为τ'=1.495τ,从而可求出τ0和τ之间的定量关系:
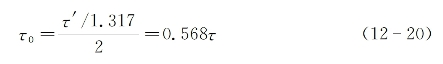
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




