非线性光学与光子学：光传输波动方程在非线性色散介质中的满足

有关光学时间孤子的早期理论研究始于20世纪70年代初。利用GVD效应去压缩自相位调制光脉冲的最早理论建议由Zeldovich与Sobelman于1971年提出［1］。几乎与此同时，Zakharov与Shabat首先在分析非线性波动方程的基础上，得出了存在具有双曲正割（sech）函数形式的时间孤子波解的结论［2］。稍后，Hasegawa与Tappert于1973年正式从理论上，分析了具有负GVD特性的光纤系统内产生时间孤子的可行性［3］。而Satsuma与Yajima则在1974年发表的理论文章中，进一步指出了一系列时间孤子解的存在，它们可用不同的正整数N=1，2，3，…来表征，并且对于除了N=1的基本孤子而言，其他高阶（N≥2）孤子在非线性介质传输过程中呈现出空间周期性变化的特性［4］。

在三阶非线性介质中，一个准单色的相干光脉冲的场振幅可一般地表示为

这里假设了光场具有均匀的横向分布，而U（z，t）为一个慢变化的脉冲包络线函数，ω0为脉冲的中心频率，k0为与ω0对应的波矢模量。在考虑到GVD效应和强脉冲引起的自相位调制效应之后，该脉冲的传输行为由以下非线性波动方程所决定［2～4］：

式中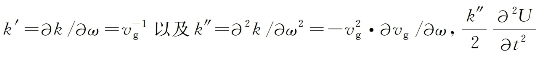，项表示GVD的影响，而右端一项则表示自相位调制的影响。从数学上可证明，只有当n2＞0以及∂υg/∂ω＞0（反常GVD），或者n2＜0以及∂υg/∂ω＜0（正常GVD）时，上述非线性波动方程才具有稳定的孤子解［2，4］。若进一步采用变量转换：(www.xing528.com)

式（12-12）可被简化为一无量纲的非线性方程：

式中，u（ξ，s）为无量纲的脉冲振幅包络线函数，ξ为无量纲的传输距离，s为无量纲的时间变量，τ0为一任意时间尺度因子，下面具体讨论上述方程对应的孤子解时，τ0将具有确定的值和物理含义。