光学双稳装置稳态理论考虑及成果

如图11-1所示的F-P干涉仪装置，其腔内包含一种透明介质，它的折射率依赖于腔内光强的变化，组成腔的两个镜面具有相同的反射率R。按照F-P干涉仪的理论，对于一个单色平面波入射光束而言，干涉仪的透射光强为［10］

式中，I0为入射光强，F=4R/（1-R）2，而δ是光束在腔内往返一次的相位移动，并可写为

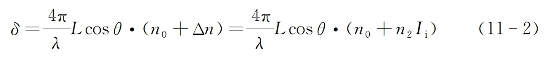
式中，λ是入射光在真空中的波长，L是腔长，θ是入射角，n0与n2分别是腔内介质的线性折射率与非线性折射率系数，Ii为腔内总光强，它包括向前和向后行进的两部分，如图11-1所示。

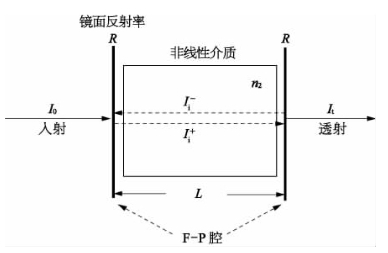
图11-1　内含非线性介质的F-P干涉仪

式（11-2）假定了介质折射率变化简单地与腔内瞬时光强成正比，这是一种稳态假设，其中腔内前向行进的光强为［10］

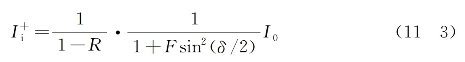
而后向行进光强为

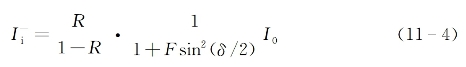
因而腔内总光强为［10，11］

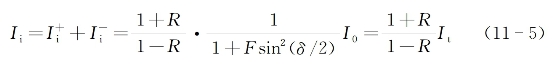
将式（11-2）和式（11-5）代入式（11-1）后可得

式中，

这里δ0为不依赖于光强的初始相位差，m为一整数且满足|δ0|≤2π。(www.xing528.com)

从式（11-6）可看出It是I0的一种隐函数。对于一个给定的I0值，It可能有多值的解，这是所以能观察到迟滞回线行为的数学根据。虽然可以用数值方法对式（11-6）进行求解，但更直观和更富于物理含义的是对该方程采用图解式求解［11，12］。为此，可从式（11-1）和式（11-5）分别求出有关干涉仪透过率的两个平行表达式：

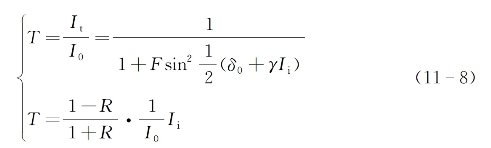
以上第一个表达式显示出透过率随（δ0+γIi）的周期性变化，而第二个表达式则代表一条在（δ0+γIi）横坐标轴上始发于δ0点的一条直线，其斜率为（1-R）/［（1+R）γI0］，亦即与I0成反比，如图11-2所示。对任意给定的入射光强I0而言，与该值对应的直线和周期性曲线的交点，即为方程式（11-6）之解。在该图中，标记为（1）～（4）的4条直线对应于4个渐次增加的I0值，它们与周期曲线的交点代表透过率的可能取值。

图11-2　用图解方法求出在不同入射光强（I0）水平下非线性F-P干涉仪的透过率

按照图11-2，知道了与不同I0值对应的透过率T值，则可进一步绘出输出/输入光强变化曲线。若将直线族的原点在横坐标上左右移动并改变它们斜率的扫描范围，则可得到在不同工作条件下的特性曲线，如图11-3所示。

图11-3　非线性双稳态装置的几种典型特征工作曲线

（a）光学开关；（b）光学微分放大；（c）光学削波；（d）光学限幅；（e），（f）光学记忆

首先解释在什么条件下可以获得如图11-3（e）和（f）所示的迟滞回线式特性曲线。为此回到图11-2假设初始相位值选定为δ0≈（π-0.87）时的情况，当I0值从接近于零（对应于直线1）增加到由直线2所表示的水平时，对应的透过率由交点A决定；当I0值增加到由直线3所代表的临界水平时，决定透过率值的是工作点B；然而I0在此水平上的哪怕微小的增加，都会使得对应直线与曲线第一个周期之前半段无交点，故工作点必须跃变至C点；当I0继续增加到由直线4所代表的输入光强极大值水平时，透过率由交点D决定。之后，当I0由其极大值逐渐减小时，决定透过率值的工作点则沿第一周期曲线后半段平滑向上移动；但当I0值减小到由直线5所代表的另一临界水平时，实际工作点将发生由E至F的跃变，这是因为I0的继续减小使得直线与曲线的交点必须移动到周期曲线的初始段。

在描述I0在0～I0max范围变化的循环过程中，工作点的移动原则是使得透过率T值尽可能发生连续的变化；除非在上述两个临界I0值时，才会发生透过率跃变式的变化。基于以上说明，对如图11-2所示的特定例子而言，其工作点随I0变化的循环过程可以借助图11-3（e）更直观地表示出来；从中可看出工作点B→C变动意味着通过率的突变式增大，而E→F点变动意味着通过率的突变式减小。图11-3（f）则显示出由图11-3（e）过程所决定的实际上能观察到的光学迟滞回线行为。

在实验中，光学双稳态装置的实际可观察到的特性曲线，将取决于具体的工作条件，如δ0，F，γ诸值的选定，入射光强度I0的水平和变化范围，透射光信号的采样方式等。

到目前为止，已经假定腔内介质对入射光波是透明的，在现实中，总存在着由于吸收或散射所造成的光损耗。假设腔内非线性介质的线性衰减系数为α0，式（11-8）可改写为［10，13］

式中，

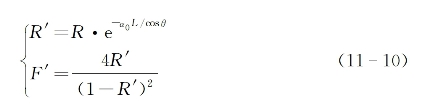
从以上两个公式可以看到，存在于非线性介质中的光损耗将导致腔镜的等效反射率变小，并使得最大透射率小于1。除这点以外，之前有关工作点移动的所有图形描述和定性讨论依然适用，特别是当α00时，式（11-9）将导致式（11-8）。